Kruskal's Algorithm

In this tutorial, you will learn how Kruskal's Algorithmworks. Also, you will find working examples of Kruskal's Algorithm in C, C++, Java and Python.

Kruskal's algorithm is a minimum spanning tree algorithm that takes a graph as input and finds the subset of the edges of that graph which

form a tree that includes every vertex has the minimum sum of weights among all the trees that can be formed from the graph.

How Kruskal's algorithm works

It falls under a class of algorithms called greedy algorithms that find the local optimum in the hopes of finding a global optimum.

We start from the edges with the lowest weight and keep adding edges until we reach our goal.

The steps for implementing Kruskal's algorithm are as follows:

• 1. Sort all the edges from low weight to high
• 2. Take the edge with the lowest weight and add it to the spanning tree. If adding the edge created a cycle, then reject this edge.
• 3. Keep adding edges until we reach all vertices.

Example of Kruskal's algorithm

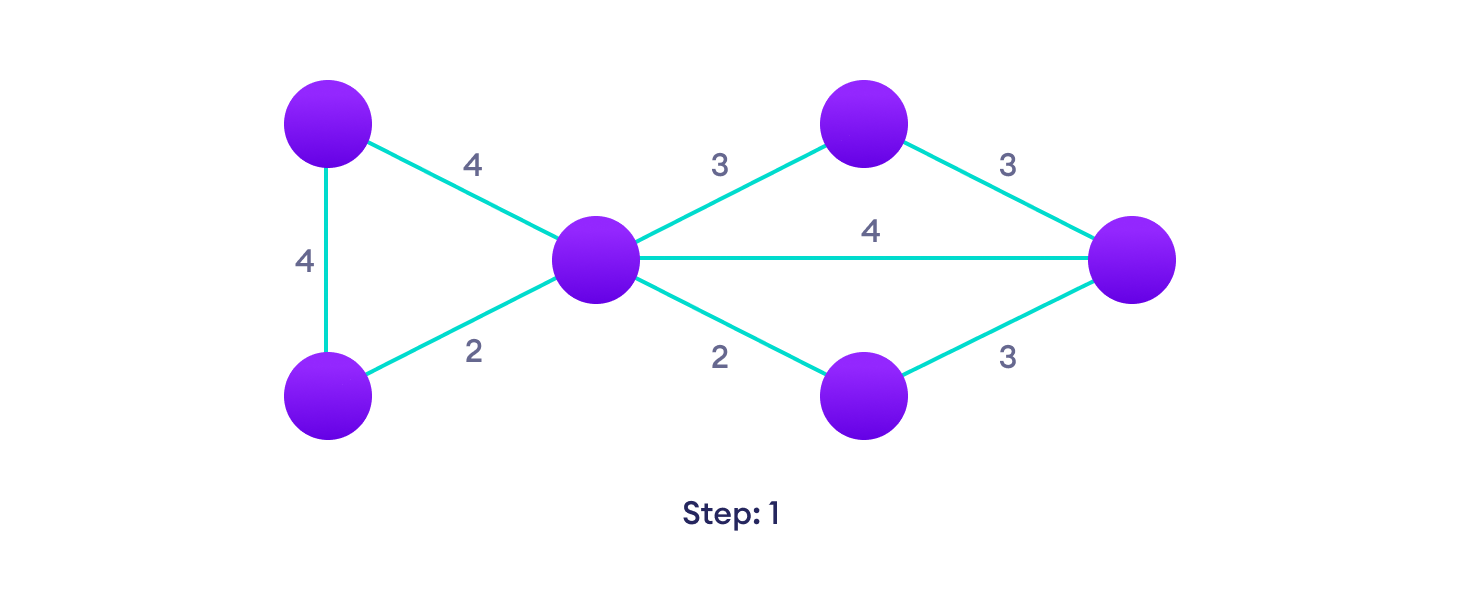Start with a weighted graph

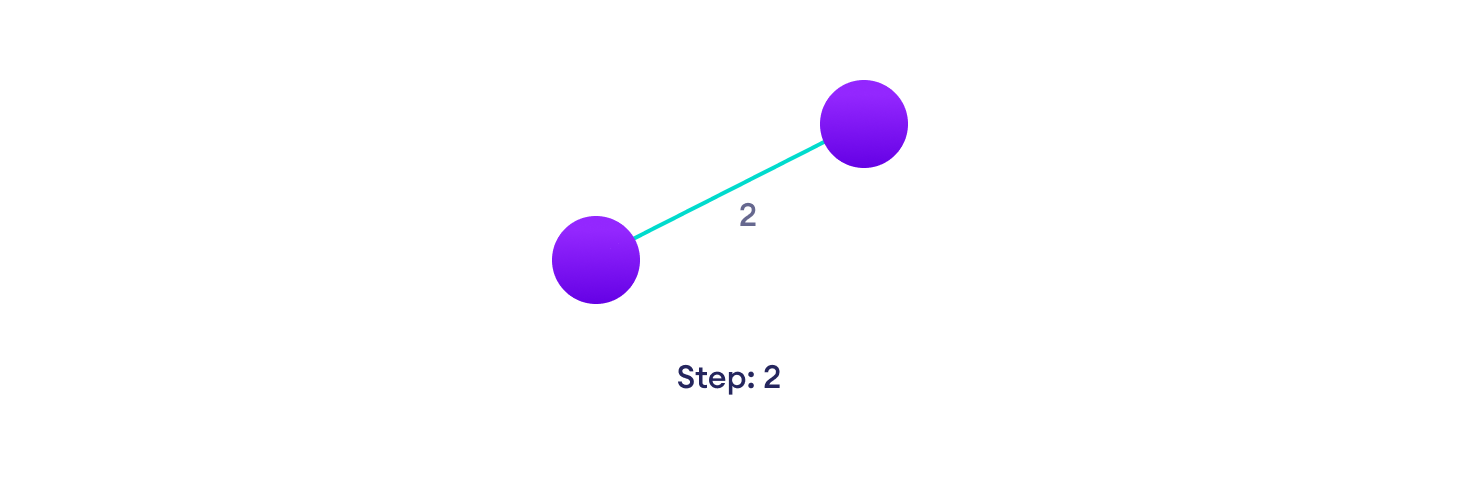Choose the edge with the least weight, if there are more than 1, choose anyone

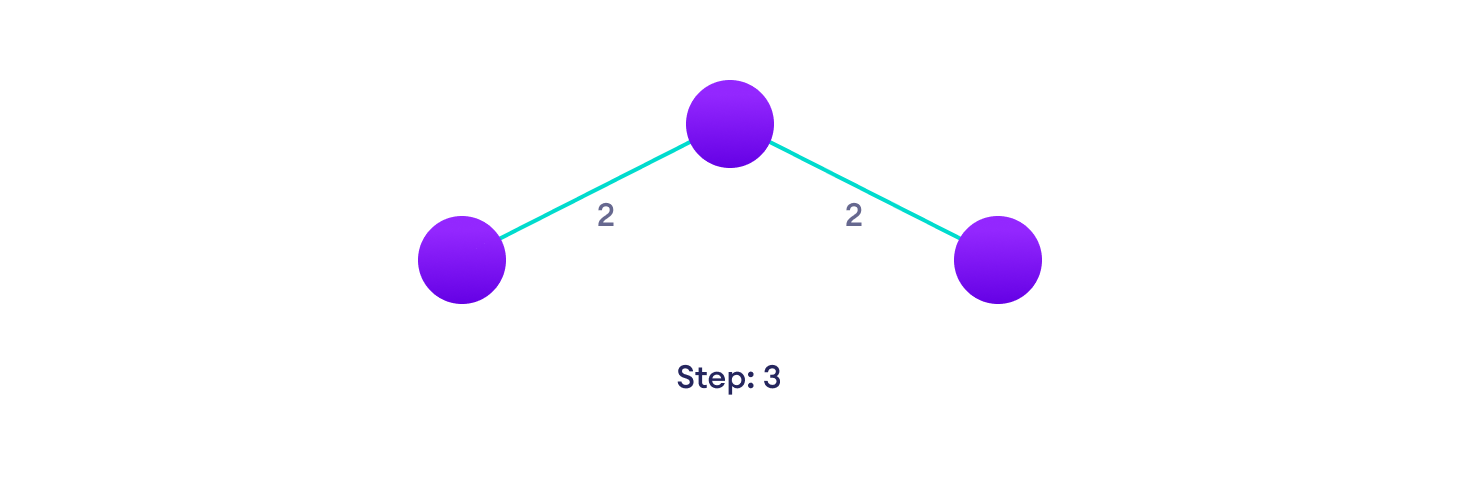Choose the next shortest edge and add it

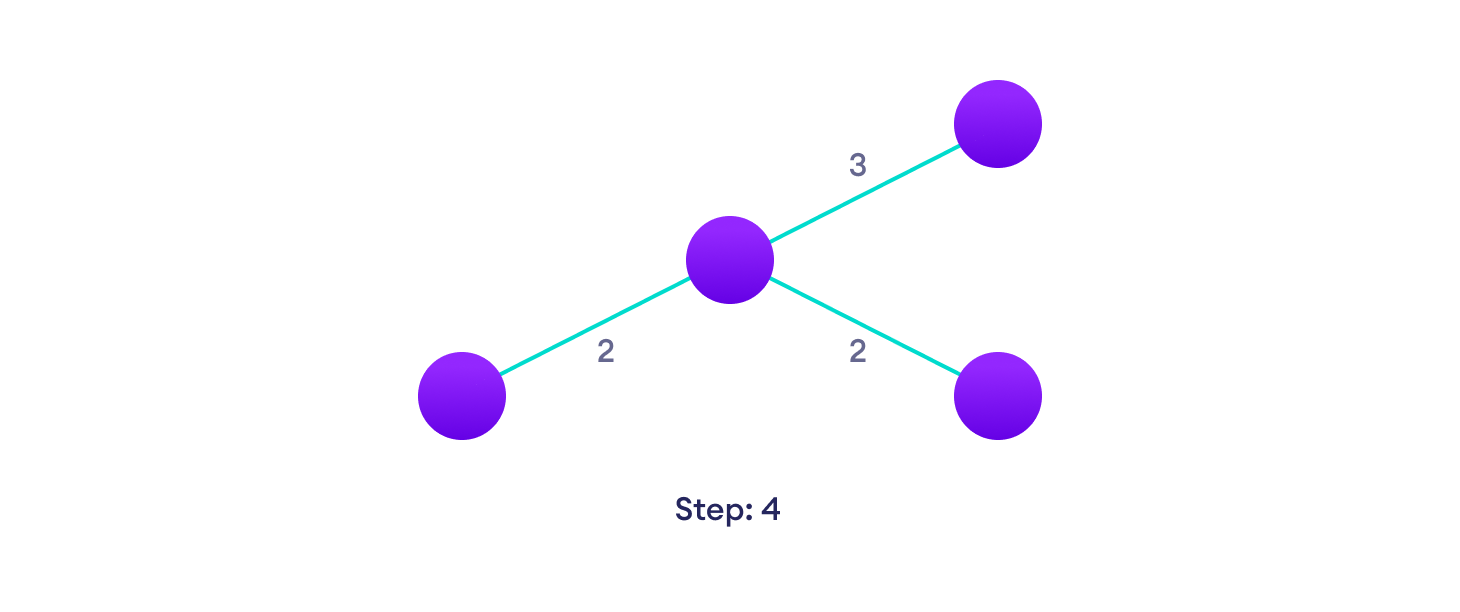Choose the next shortest edge that doesn't create a cycle and add it

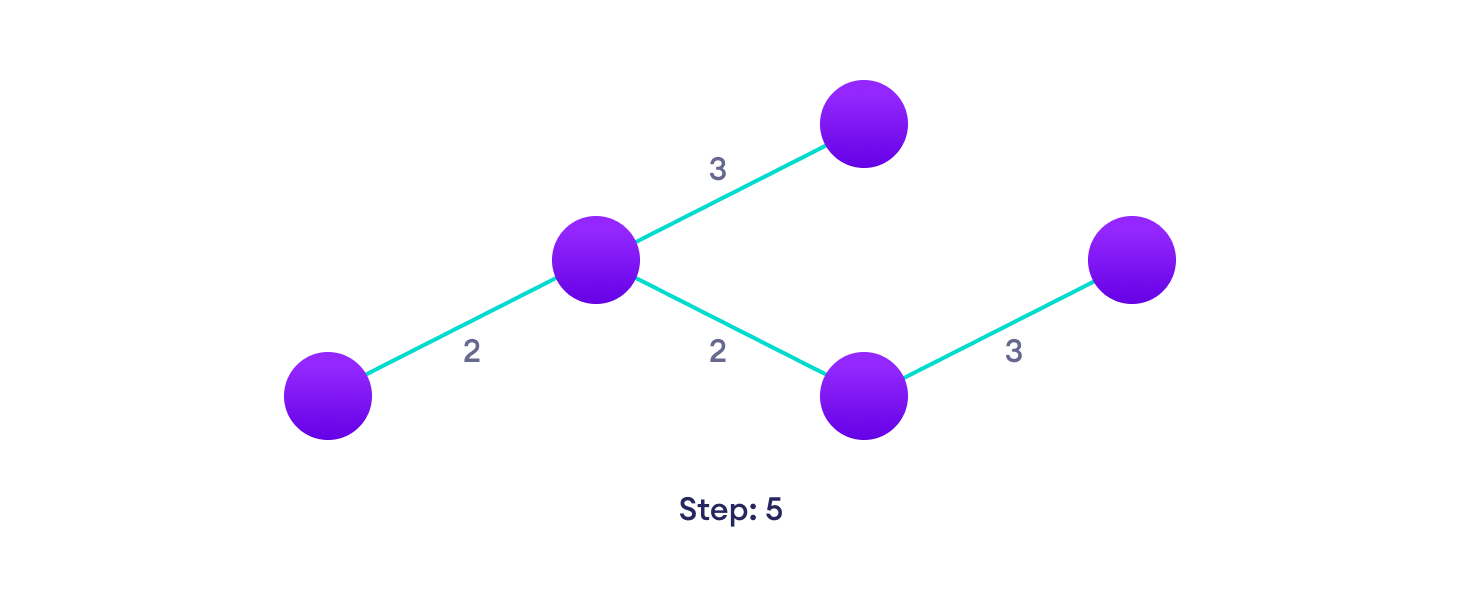Choose the next shortest edge that doesn't create a cycle and add it

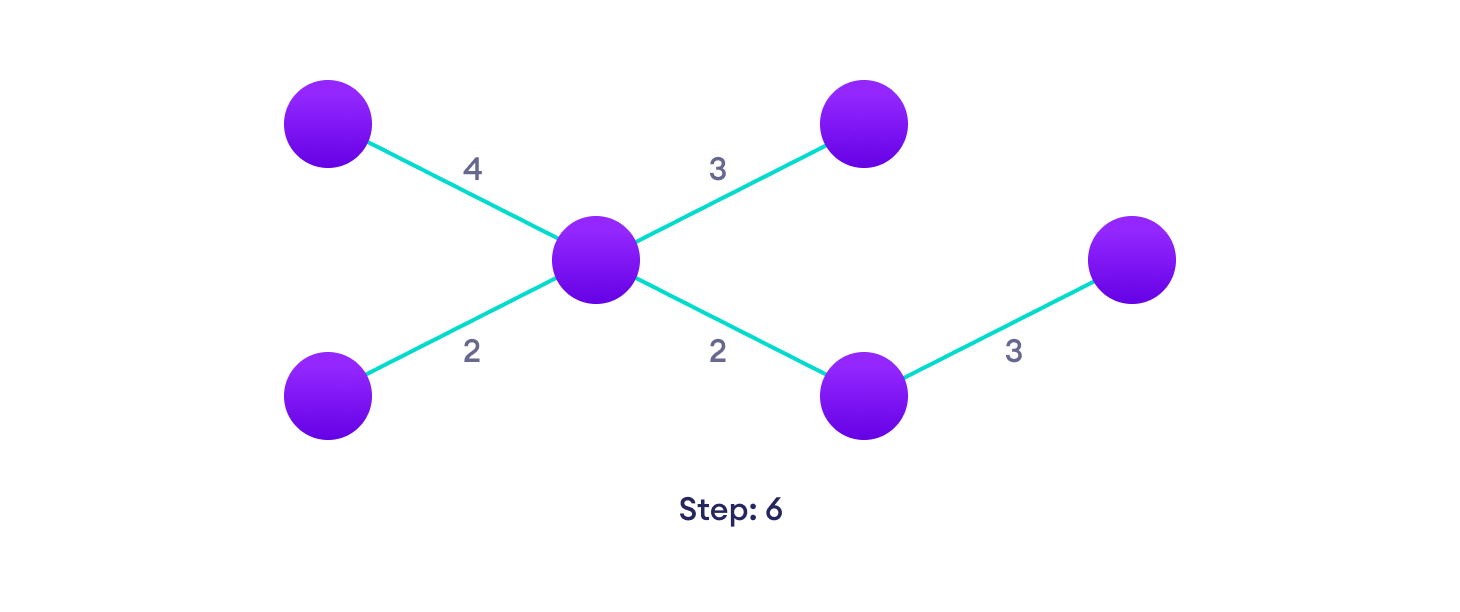Repeat until you have a spanning tree

Kruskal Algorithm Pseudocode

Any minimum spanning tree algorithm revolves around checking if adding an edge creates a loop or not.

The most common way to find this out is an algorithm called Union FInd. The Union-Find algorithm divides the vertices into clusters and allows us to check if two vertices belong to the same cluster or not and hence decide whether adding an edge creates a cycle.

Kruskal Implementations

Kruskal Algorithm - Java Implementation

Kruskal Algorithm - Python Implementation

Kruskal's vs Prim's Algorithm

Prim's algorithm is another popular minimum spanning tree algorithm that uses a different logic to find the MST of a graph. Instead of starting from an edge, Prim's algorithm starts from a vertex and keeps adding lowest-weight edges which aren't in the tree, until all vertices have been covered.

Kruskal's Algorithm Complexity

The time complexity Of Kruskal's Algorithm is: O(E log E).

Kruskal's Algorithm Applications

In order to layout electrical wiring In computer network (LAN connection)

Reference:

• https://www.programiz.com/dsa/kruskal-algorithm