Counting Sort

Counting sort is a sorting technique based on keys between a specific range. It works by counting the number of objects having distinct key values (kind of hashing). Then do some arithmetic to calculate the position of each object in the output sequence.

Characteristics of counting sort:

• Counting sort makes assumptions about the data, for example, it assumes that values are going to be in the range of 0 to 10 or 10 – 99 etc, Some other assumptions counting sort makes are input data will be all real numbers.
• Like other algorithms this sorting algorithm is not a comparison-based algorithm, it hashes the value in a temporary count array and uses them for sorting.
• It uses a temporary array making it a non In Place algorithm.

Let us understand it with the help of an example.

• For simplicity, consider the data in the range 0 to 9.
• Input data: {1, 4, 1, 2, 7, 5, 2}
• Take a count array to store the count of each unique object.

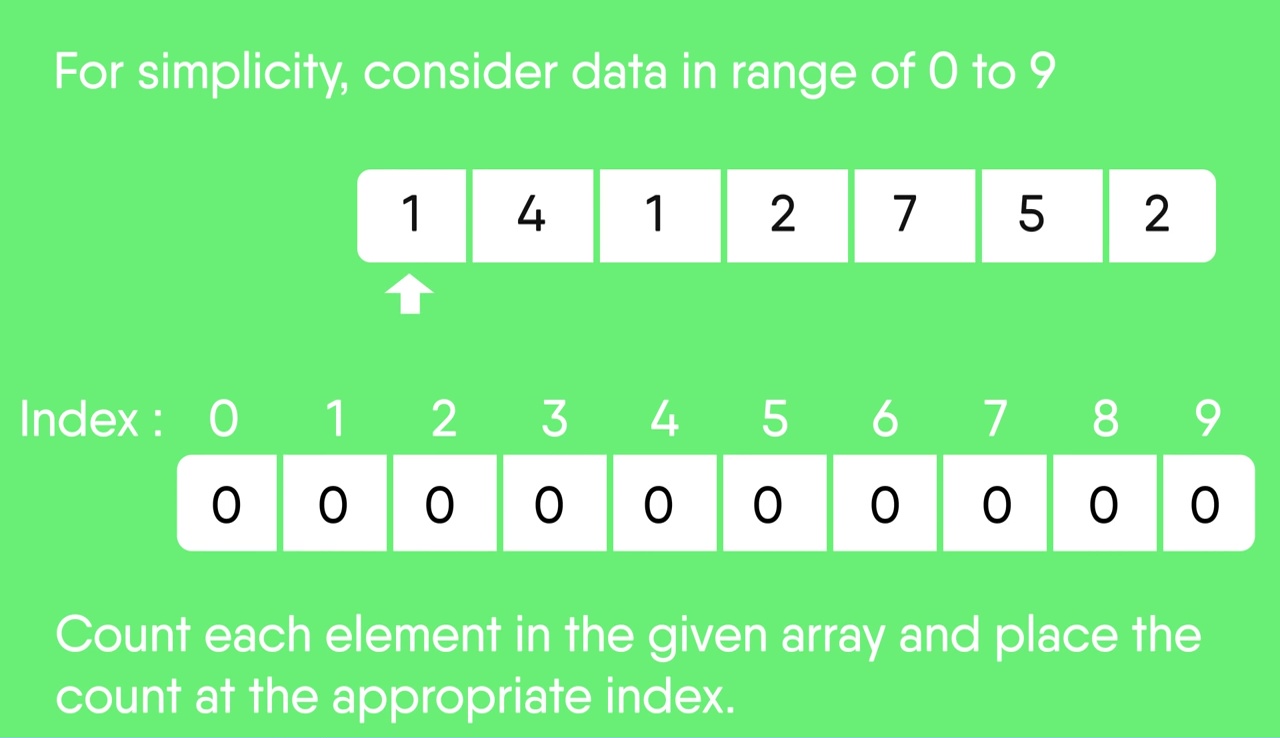
Now, store the count of each unique element in the count array If any element repeats itself, simply increase its count.

Here, the count of each unique element in the count array is as shown below: Index: 0 1 2 3 4 5 6 7 8 9 Count: 0 2 2 0 1 1 0 1 0 0

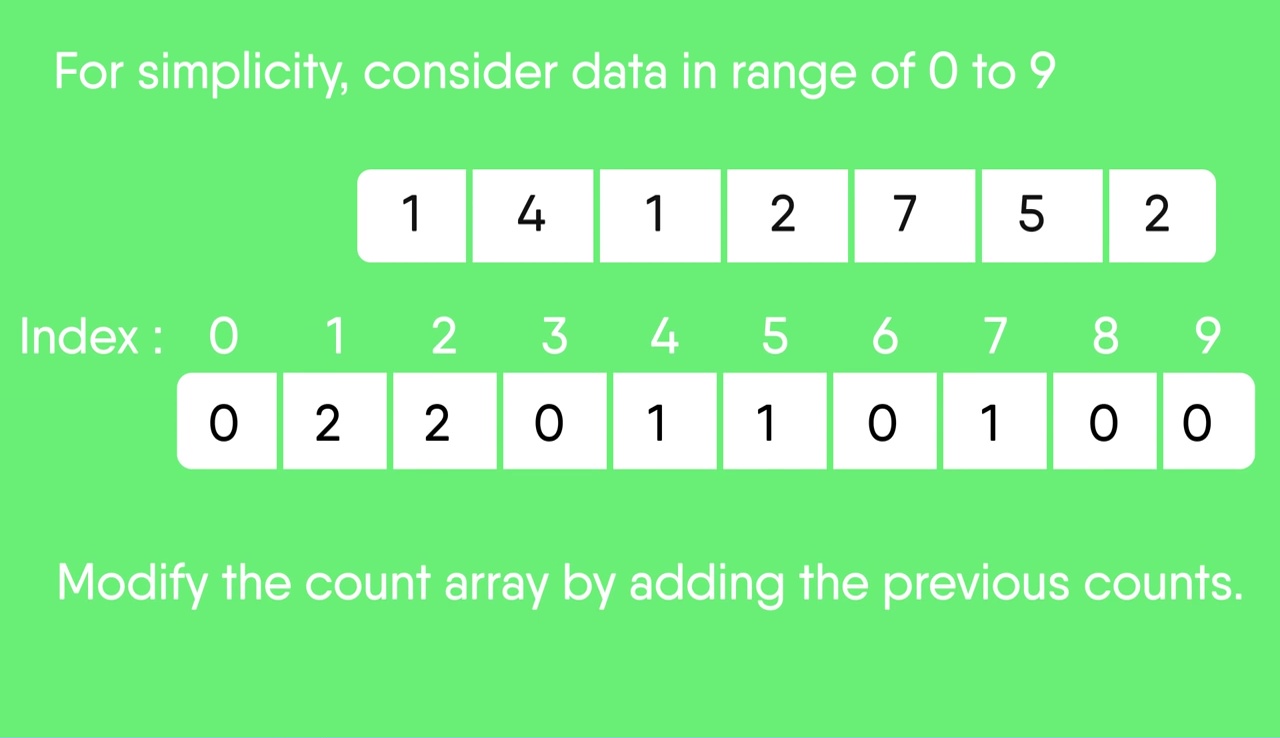
Modify the count array such that each element at each index stores the sum of previous counts. Index: 0 1 2 3 4 5 6 7 8 9 Count: 0 2 4 4 5 6 6 7 7 7 The modified count array indicates the position of each object in the output sequence. Find the index of each element of the original array in the count array. This gives the cumulative count.

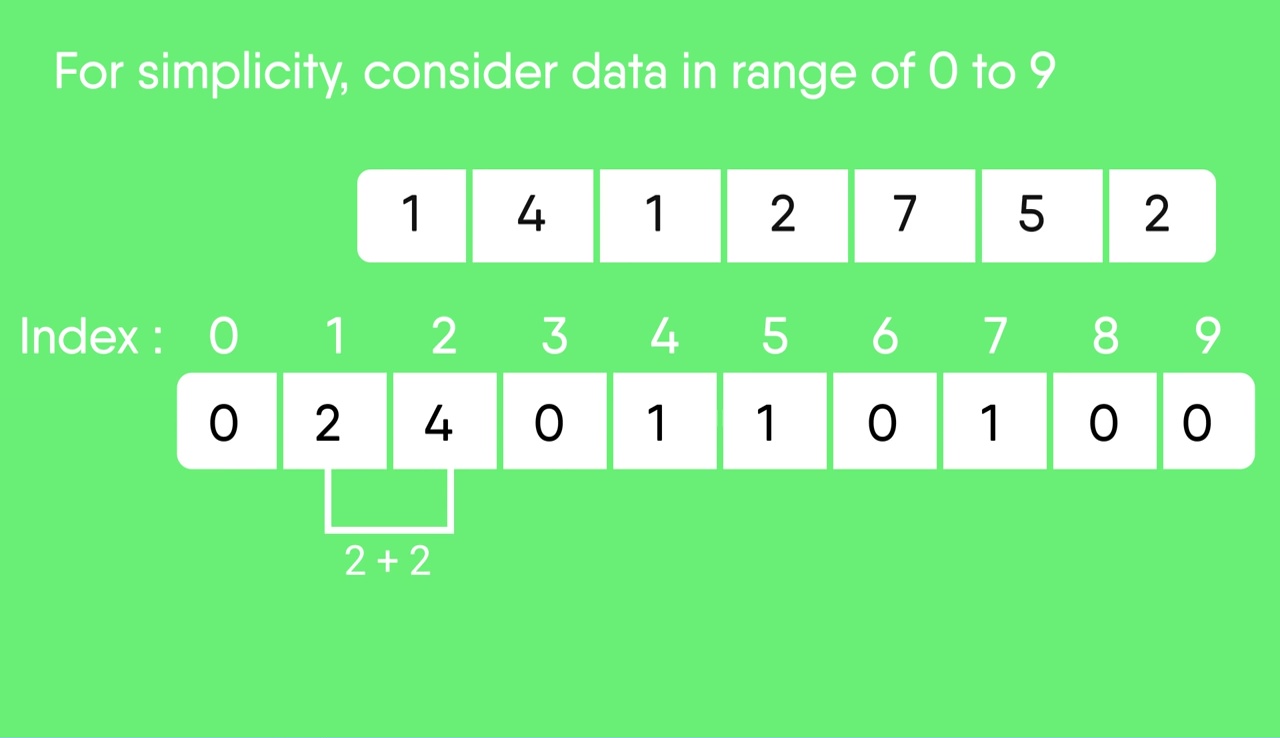
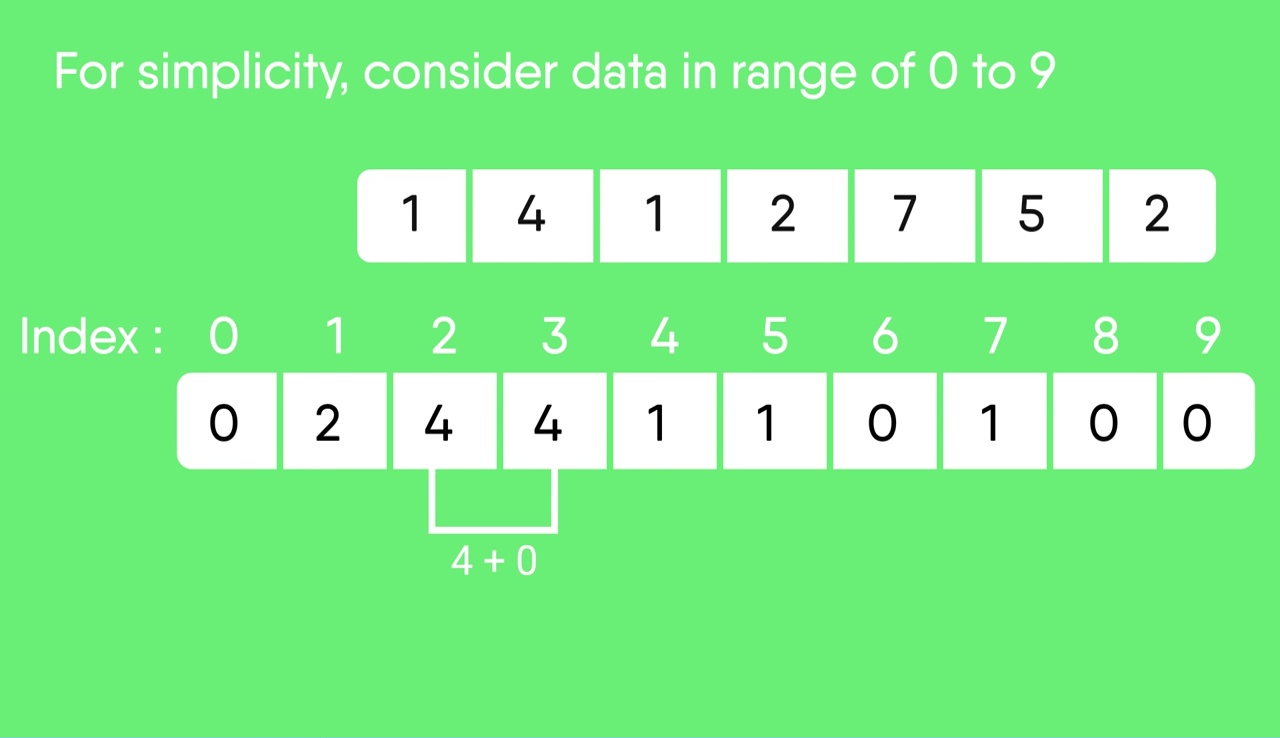
Rotate the array clockwise for one time. Index: 0 1 2 3 4 5 6 7 8 9 Count: 0 0 2 4 4 5 6 6 7 7

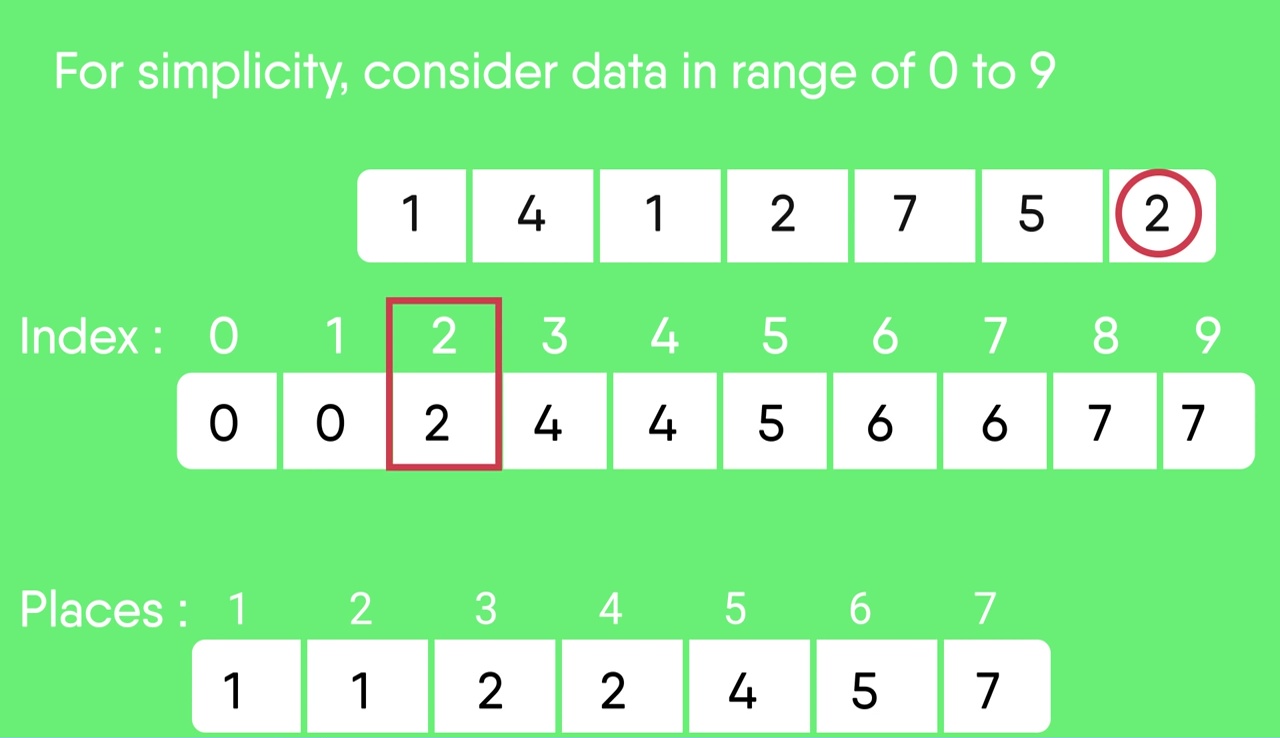
• Output each object from the input sequence followed by increasing its count by 1.
• Process the input data: 1, 4, 1, 2, 7, 5, 2. Position of 1 is 0.
• Put data 1 at index 0 in output. Increase count by 1 to place next data 1 at an index 1 greater than this index.

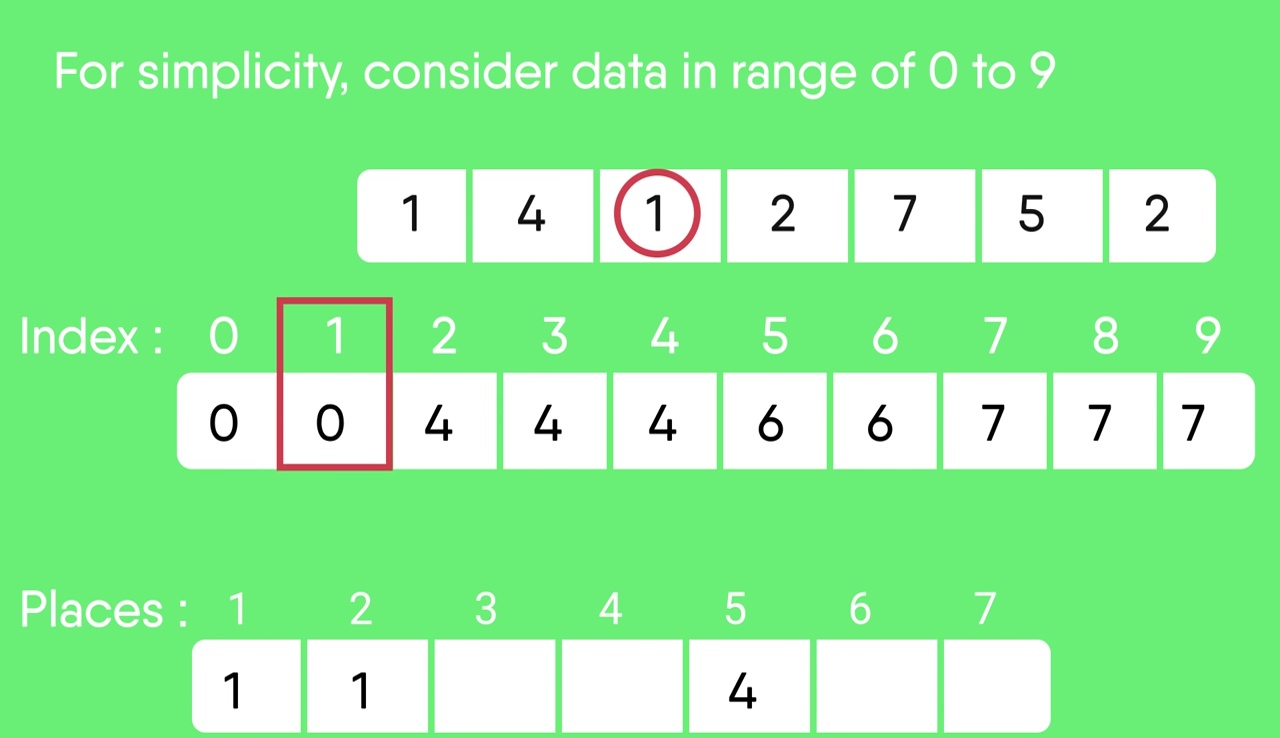
• After placing each element at its correct position, decrease its count by one.

Strengths & Weaknesses

The High-Level Idea

Counting sort works by iterating through the input, counting the number of times each item occurs, and using those counts to compute an item's index in the final, sorted array.

Counting How Many Times Each Item Occurs

Say we have this array:

Building the Sorted Output

Now that we know how many times each item appears, we can fill in our sorted array. Looking at counts, we don't have any 0's or 1's, but we've got two 2's. So, those go at the start of our sorted array.

And, with that, we're done!

Final sorted output: [2, 2, 4, 4, 6, 8, 9, 9, 9].

Building a Next Index Array

Using our counts array, we can pre-compute where each item from the input should go. Then we'll just iterate through the input, using the pre-computed indices to place each item in the right spot.

We'll use our counts array to build up another array, nextIndex, that will track where the next occurrence of a price goes in our sorted output. For instance, nextIndex[4] would hold the index for the next item with a price of $4.

Hold up. Doesn't this add O(k)O(k) space to our algorithm?

Hang tight ... we'll see that with some cleverness we won't need a separate array for nextIndex after all.

We can initialize nextIndex from our counts array.

The lowest price is $2, so the $2 items will start at index 0. (Nothing costs $0 or $1, so we'll just set those to 0.)

Items that cost $3 go after all the items that cost $2. Two items in the array cost $2, so they'll take up indices 0 and 1. That means the first $3 item would go at index 2.

Notice how nextIndex[3] = nextIndex[2] + counts[2]. That makes sense, because we're taking the starting point for the items and moving forward to make room for each of them. In general:

nextIndex[i] = nextIndex[i - 1] + counts[i - 1]

We can keep iterating through counts using this formula to fill in nextIndex.

As we'll see, we actually don't need counts anymore after we've built nextIndex.

So instead of creating a separate array for nextIndex, we can just modify counts in-place in one pass to get our nextIndex array. It's slightly trickier, but it can be done :)

Building Our Sorted array With nextIndex

Complexity

Counting sort takes O(n + k)O(n+k) time and O(n + k)O(n+k) space, where nn is the number of items we're sorting and kk is the number of possible values.

We iterate through the input items twice—once to populate counts and once to fill in the output array. Both iterations are O(n)O(n) time. Additionally, we iterate through counts once to fill in nextIndex, which is O(k)O(k) time.

The algorithm allocates three additional arrays: one for counts, one for nextIndex, and one for the output. The first two are O(k)O(k) space and the final one is O(n)O(n) space.

You can actually combine counts and nextIndex into one array. No asymptotic changes, but it does save O(k)O(k) space.

In many cases cases, k is O(n) (i.e.: the number of items to be sorted is not asymptotically different than the number of values those items can take on. Because of this, counting sort is often said to be O(n) time and space.

Reference:

https://www.geeksforgeeks.org/counting-sort/?ref=lbp https://www.interviewcake.com/concept/java/counting-sort