Berechnung der Straßenlänge aus geographischen Koordinaten - DarioDagne/OSM-Analysis GitHub Wiki
Die OSM-Daten basieren auf einem geografischen Koordinatensystem, welches Angaben über die geographische Breite (Latitude) und die geographische Länge (Longitude) beinhaltet.
Die geografischen Koordinaten sind mathematisch gesehen Kugelkoordinaten, mit denen sich die Lage eines Punktes auf der Erdoberfläche beschreiben lässt [3].
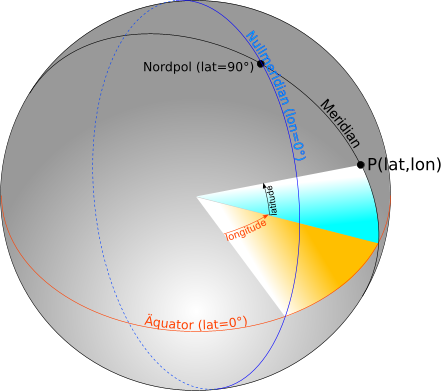
Dabei wird die geographische Breite vom Äquator aus nach Norden (0° am Äquator, 90° am Nordpol) bzw. nach Süden (0° am Äquator, 90° am Südpol) und die geographische Länge vom willkürlich festgelegten Nullmeridian (welcher durch die Londoner Sternwarte Greenwich definiert wird) jeweils von 0° bis 180° nach Osten bzw. Westen.
Abb. 1: Definition eines Punktes auf der Erdoberfläche durch geographische Länge und Breite [4]
Zur genaueren Beschreibung werden die Längen- und Breitengrade zusätzlich in Minuten und Sekunden unterteilt. Demnach erhält man eine Koordinatendarstellung nach der Form 45°17'06.70''N 8° 0'55.33'' O. Alternative Schreibweisen nutzen die intuitivere Dezimalschreibweise.
Von dem Sexagesimalformat abweichend werden die Koordinaten in der OSM-Datenbank als Dezimalgrade angegeben. Hierbei wurden zusätzlich Konventionen (siehe [5]) getroffen, welche die Angabe der Information über die Himmelsrichtung nichtig machen. Lediglich eine Unterscheidung in Breiten- bzw. Längengrade (lat bzw. lon) ist zwingend erforderlich um eine Verwechslung auszuschließen. An einem Beispiel lässt sich zeigen, wie die Datenbank die Information über die geographischen Koordinaten eines Punktes (node) auf der Erdoberfläche speichert:
<node id="25496583" lat="51.5173639" lon="-0.140043" version="1" changeset="203496" user="80n" uid="1238" visible="true" timestamp="2007-01-28T11:40:26Z"> <tag k="highway" v="traffic_signals"/> </node>
Hier wird zunächst eine eindeutige Knoten-ID vergeben, anschließend werden Die Längen- und Breitenangaben als Dezimalzahl abgespeichert. Die nachfolgende Tabelle soll einen Überblick über die möglichen Werte liefern:
Tabelle 1: Definition eines Knotens in OSM [5]
| Name | Wert | Beschreibung |
|---|---|---|
| id | 64-bit-Integer > 0 | Eindeutige ID für jeden Knoten |
| lat | Dezimalzahl -90.0000000 <= lat <= 90.0000000 mit 7 Nachkommastellen | Breitengrade in Dezimalschreibweise. Konventionell stehen positive Werte für Norden und negative für Süden. |
| lon | Dezimalzahl -18.0000000 <= lon <= 180.0000000 mit 7 Nachkommastellen | Längengrade in Dezimalschreibweise Konvention: positive Koordinaten = Osten, negative Koordinaten = Westen |
| tags | Zeichenketten | Set von Schlüssel-Werte-Paaren für zusätzliche Angaben |
Anders als bei der algebraischen Berechnung vom Abstand zweier Punkte in katesischen Koordinaten muss bei Verwendung von geographischen Koordinaten eine gewisse Idealisierung getroffen werden. Je nach gewünschter Genauigkeit und verfügbarer Rechenkapazität gibt es hierfür verschiedene Modelle. Wir beschränken uns hierbei zunächst auf Modelle, welche von einer kugelförmigen Erdoberfläche ausgehen. Diese Annahme ist für kurze Distanzen allemal hinreichend, ignoriert aber den Fakt, dass die Erde eigentlich ein Rotationsellipsoid ist.
Für kurze Distanzen in Äquatornähe verlaufen die Längen- und Breitengrade nahezu senkrecht (siehe Abb. 2). Dies ermöglicht eine Projektion der Erdoberfläche auf eine Ebene und die Verwendung eines kartesischen Koordinatensystems für algebraische Berechnungen.
Abb. 2: Einfache Berechnung von Entfernungen mittels Satz des Pythagoras
Zur Nutzung dieser einfachen Berechnung wird von einem konstanten Abstand der Längen- und Breitengrade ausgegangen:
- Abstand zweier Breitengrade (1° Unterschied): 111 km
- Abstand zweier Längengrade (1° Unterschied): 71,5 km
Laut [6] ist die Annahme eines konstanten Abstandes der Breitengrade voneiander dabei nahezu korrekt, diese schwanken lediglich durch die (hier ignorierte) Erdabplattung an den Polen, sodass der Abstand zwischen 2 Breitengraden am Äquator mit 110,574 km pro Grad etwas geringer ist als an den Polen (111,694 km pro Grad) [6].
Die Längengrade dagegen haben naturgemäß keinen konstanten Abstand. Am Äquator beträgt dieser ca. 111,319 km, dieser Abstand schrumpft jedoch bis zu den Polen, an welchen die Längengrade einander schneiden, hier beträgt der Abstand 0 km. Für Deutschland kann gemittelt von den oben angegebenen 71,5 km ausgegangen werden. Hier wird jedoch auch die Grenze dieser einfachen Methode deutlich. Bei größeren Distanzen ist die Implizierte Rechtwinklichkeit zwischen den Längen- und Breitengraden sowie der konstante Abstand der Längengrade schlichtweg nicht mehr gegeben, sodass die berechnete Strecke verfälscht wird. Außerdem setzt die Berechnung die Kenntniss einer Abschätzung für den Abstand zweier Längengrade im untersuchten Bereich voraus.
Soll die Entfernung zweier Punkte wie in Abb. 2 gezeigt berechnet werden, so liefert diese vereinfachte Methiode dafür den Ansatz
// Koordinaten (lat1,lon1) und (lat2,lon2) in km
dx = 71.5 * (lon2 - lon1)
dy = 111 * (lat2 - lat1)
laenge = sqrt(dx * dx + dy * dy)
Die erste Methode ist aufgrund der festen Werte für den Abstand zweier Längengrade sehr unflexibel und somit wenig brauchbar für eine allgemeingültige Implementierung. Dieser Fehler kann aber durch die Definition des Abstandes über eine trigonometrische Interpolation zwischen dem Äquatorabstand (111.319 km) und dem Abstand der Längenkreise an den Polen (0km) ausgeglichen werden [4]. Somit kann der Pseudocode aus dem vorherigen Beispiel erweitert werden zu:
// Koordinaten (lat1,lon1) und (lat2,lon2) in km
// Abstaende zwischen Längen- und Breitengraden:
d_lat = 111
d_lon = 111 * cos((lat1+lat2)/2)
dx = d_lon * (lon2 - lon1)
dy = d_lat * (lat2 - lat1)
laenge = sqrt(dx * dx + dy * dy)
Dieser Ansatz versagt nachwievor bei großen Entfernungen und Punkten nahe den Polen, hat aber eine höhere Genauigkeit und übernimmt die Berechnung der zuvor konstanten Längenkreis-Abstände.
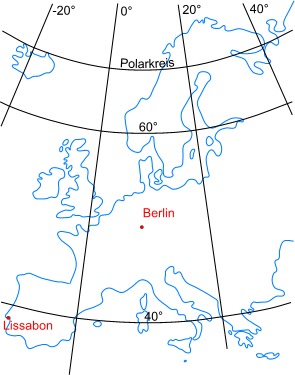
Die beiden zuvor vorgestellten Ansätze gehen beide von einem rechtwinkligen Gitternetz aus. Diese Annahme ist auf einem größeren Maßstab (z.B. einer Europakarte) jedoch nicht mehr haltbar, wie aus Abb. 3 hervorgeht.
Abb. 3: Fehlende Rechtwinkligkeit des Gitternetzes am Beispiel einer Europakarte [4]
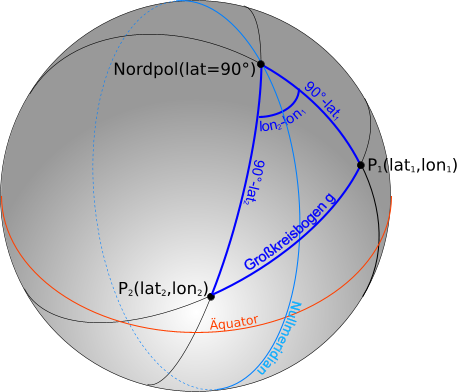
Um hier brauchbare Ergebnisse zu erhalten, muss die sphärische Trigonometrie bemüht werden. Der Abstand zweier Punkte auf der Erdkugel ist jetzt durch einen sogenannten Großkreisbogen definiert. Dieser bildet mit dem Nordpol ein Kugeldreieck, von welchem zwei Seiten und ein Winkel bekannt sind.
Abb. 3: Berechnung des Abstandes zweier Punkte mittels Kugelkoordinaten [4]
Die Seiten ergeben sich aus dem Abstand der Punkte P1 und P2 vom Nordpol, also aus deren Breitengraden. Der eingeschlossene Winkel lässt sich aus der Differenz der beiden Längengrade bestimmen. Unter Verwendung des Seitenkosinussatzes leitet Kompf daraus die folgende Berechnung der Strecke g (kürzester Abstand zwischen den Punkten P1 und P2) her:
laenge = 6378.388 * acos(sin(lat1) * sin(lat2) + cos(lat1) * cos(lat2) * cos(lon2 - lon1))
Dabei steht der konstante Wert 6378.388 für den Erdradius in km.
Ziel unserer eigenen Implementierung ist eine individuelle Berechnung von Straßenlängen anhand der gegebenen Knoten-Koordinaten. Zwar existiert in OSM ein distance-key, dieser kann allerdings aufgrund verzweigter Straßen nur sehr selten für unsere Anwendung eingesetzt werden. Die Nutzung einer bounding box zur Eingrenzung des untersuchten Bereichs führt zudem zu dem Problem, dass Straßen, welche einzelne Städte verbinden aufgetrennt werden. Insbesondere Autobahnen und Bundesstraßen sollten nicht vollständig ins Straßennetz einer Stadt zählen, wenn sie diese durchqueren.
In der finalen Implementierung sollen Daten, welche durch _Nominatim _und _Overpass _geliefert werden (siehe parallele Arbeit von Herrn Jonaca) als Ausgangspunkt für diese Berechnungen dienen. Für erste Tests wird jedoch eine eigene node-Klasse erstellt, welche lediglich die Längen-und Breitengrade eines Punktes sowie eine optionale Beschreibung beinhaltet.
In der distance-Prozedur wird je nach gewählter Methode (Legende siehe Tabelle 2) die Entfernung zwischen den beiden angegebenen Knoten ermittelt und über eine Konsolenausgabe zurückgegeben.
Tabelle 2: Berechnungsmodelle und zugehörige IDs
| method-ID | Berechnungsmodell |
|---|---|
| 1 | Einfache Berechnung mittels Satz des Pythagoras |
| 2 | Erweitertes Berechnungsmodell mit variablem Abstand der Längengrade |
| 3 | Berechnung mittels Kugelkoordinaten |
Zum Testen der drei implementierten Methoden wurden mehrere Knoten erstellt und der Abstand zwischen diesen mit allen drei verfügbaren Methoden berechnet:
var Entfernung_kurz = new Entfernungsberechnung("kurze Strecke",Node_Metallkunde,Node_Lampadiusbau);
var Entfernung_mittel = new Entfernungsberechnung("mittlere Strecke", Node_TUBAF,Node_TUCH);
var Entfernung_lang = new Entfernungsberechnung("lange Strecke", Node_TUBAF,Node_Oxford);
Entfernungsberechnung[] Strecken = new Entfernungsberechnung[3]{Entfernung_kurz, Entfernung_mittel, Entfernung_lang};
foreach (Entfernungsberechnung Strecke in Strecken)
{
Console.WriteLine($"{Strecke.name}: ");
for (uint model = 1; model<=3; model++)
{
Strecke.distance(model);
}
}
Dabei wurden für die Knoten Node_TUBAF, Node_TUCH, Node_Metallkunde, Node_Lampadiusbau und Node_Oxford folgende reale Koordinaten mittels OpenStreetMap bzw. Google Maps ermittelt:
Tabelle 3: Koordinaten der Testpunkte
| Name | Erklärung | lat | lon |
|---|---|---|---|
| Node_TUBAF | Universitätshauptgebäude TU Freiberg | 50.9181009 | 13.3409753 |
| Node_TUCH | Universitätshauptgebäude TU Chemnitz | 50.8398942 | 12.9278649 |
| Node_Metallkunde | Haus Metallkunde (Universitätsgebäude TUBAF) | 50.9243187 | 13.3316376 |
| Node_Lampadiusbau | Lampadiusbau (Universitätsgebäude TUBAF) | 50.9247312 | 13.3302340 |
| Node_Oxford | Universität Oxford | 51.7589021 | -1.2536706 |
Aus diesen Knoten wurden 3 Teststrecken zusammengesetzt und die Abstände zwischen jeweils 2 Knoten ermittelt. Zum Vergleich wurde jeweils auch die Strecke via Google Maps ausgemessen. Daraus ergeben sich die nachfolgenden Strecken (siehe Tabelle 4).
Tabelle 4: Ergebnisse der Teststreckenberechnung
| Streckenname | Knoten 1 | Knoten 2 | Länge Google Maps | Länge Methode 1 | Länge Methode 2 | Länge Methode 3 |
|---|---|---|---|---|---|---|
| Entfernung_kurz | Node_Metallkunde | Node_Lampadiusbau | 0,109 km | 0,110 km | 0,108 km | 0,109 km |
| Entfernung_mittel | Node_TUBAF | Node_TUCH | 30,260 km | 30,787 km | 30,207 km | 30,295 km |
| Entfernung_lang | Node_TUBAF | Node_Oxford | 1016,41 km | 1047,682 km | 1016,341 km | 1017,585 km |
Aus der obigen Tabelle geht hervor, dass alle 3 Rechenmodelle gute Ergebnisse liefern.Für kurze Distanzen reicht bereits ein planarer Ansatz, hier kann die Erdkrümmung vernachlässigt werden. Bei größeren Distanzen sollte diese berücksichtigt werden. Für die Auswertung von Straßenlängen ist jedoch mit sehr geringen Distanzen zwischen den Knoten zu rechnen, sodass hier auch die zweite Methode angewendet werden kann. Angestrebt wird für den finalen Algorithmus eine automatisierte Entscheidung für eine der beiden Methoden in Abhängigkeit von der zu messenden Entfernung. Die erste Methode mit konstantem Längengrad wird aufgrund ihrer Inflexibilität nicht berücksichtigt.
Für die Berechnung der Strecke einer Straße wurde eine eigenständige Klasse CalculateDistance angelegt. In dieser wurden zwei der oben aufgeführten Methoden zur Berechnung des Abstands zweier geographischer Koordinaten als EstimateDistancePythagoras und EstimateDistanceSphericalCoordinates umgesetzt. Diese beiden Methoden wurden lokal gesetzt. Von außen ist über eine Instant der erstellten Klasse nur die Methode CalculateNetLength ansprechbar, welche eine Schleife über alle ways eines Straßennetzes ausführt und entscheidet, welche der beiden Berechnungsgrundlagen für die jeweilige Auswertung eingesetzt werden soll. Hierbei ist der Abstand zu den Polen ausschlaggebend für die Entscheidung, ob mit Kugelkoordinaten gerechnet wird oder nicht. Der Aufbau dieser Methode ist im nachfolgenden Ablaufplan(Abb. 4) umrissen.
Abb. 4: Aktivitätsdiagramm CalculateNetLength-Methode
Für die Klasse CalculateDistance ergibt sich das folgende UML-Diagramm:
Abb. 5: UML-Diagramm CalculateDistance-Klasse.
Diese Klasse wurde wie hier dargestellt in das bestehende UML-Diagramm eingegliedert. Dabei ermöglicht die Vererbung von der LoadData-Klasse eine Nutzung der dort implementierten Source(), welche eine datentypunabhängige Nutzung von Osm-Dateien ermöglicht.
Folgendes Beispiel zeigt die Berechnung der Länge der Lessingstraße in Freiberg unter Verwendung heruntergeladener OSM-Daten:
/* Dieses Beispiel setzt eine Datei 'freiberg.xml' voraus.
Zudem wurde hier bereits ein Objekt der Klasse 'filtered City' angelegt.
Diese kann unter Verwendung der Klasse OsmDataSearch heruntergeladen werden.
*/
string filename = @"freiberg.xml";
string strasse = "Lessingstraße";
double length = 0.0;
var Calc = new CalculateDistance(filename); // Anlegen einer neuen Klasseninstanz
length = Calc.CalculateNetLength(filteredCity.GetspecificWay(strasse)); // Abrufen des Datensatzes für die gewählte Straße + Berechnung der Länge
Console.WriteLine($"Länge = {length} km"); // Ausgabe
// Ausgabe: 'Länge = 1,124 km'
Das Ergebnis aus diesem Beispiel wurde anhand einer Messung auf Google Maps (Screenshot) verifiziert.