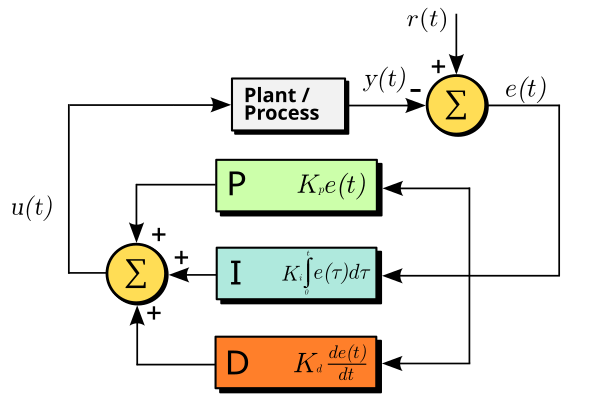
PID control is a form of closed-loop control that determines its output based on the difference between the current value of a variable and the desired value. An advantage of the PID controller is that it requires no knowledge of the process it is attempting to control. All that is needed is a simple calibration of up to 3 coefficients.

PID stands for "Proportional-Integral-Derivative". These refer to the three terms in the equation for determining the output of the controller.

The proportional term is simply the difference between the input and the setpoint multiplied by a calibrated coefficient, Kp. This will get the output most of the way, but will hold just below the desired setpoint. As the setpoint is approached, the error goes to 0, which would in turn drive the output to 0. For this reason, the integral term is used.

By adding a constant term to the proportional control, one can tune the controller to eliminate the error after a steady-state is reached. However, once a disturbance is introduced to this system, it will never recover back to the set point; there will always be an offset error.

The integral term consists of a coefficient, Ki, multiplied by the time integral of the error. This allows the controller to drive the process all the way to the setpoint, with little error.

As long as some error is present, the integral of that error will be changing. This means that a steady-state cannot be reached until the point value is equal to the set point.

With P and I, the setpoint can be reached, but there will often be significant overshoot. A derivative term can significantly reduce overshoot and settling time. The derivative term is another coefficient, Kd, multiplied by the slope of the error over time. Derivative terms are not always used as they are sensitive to noise and can cause stability problems.

###Response to disturbance

For the most precise tuning, software tools can be purchased to calculate the necessary coefficients. This can be expensive however, and for simple/low-cost systems, manual tuning is often used. For a quick, rule-of-thumb calculation, the Ziegler-Nichols method can be used:

With Ki and Kd set to zero, increase Kp until the output begins to oscillate. The Kp at this point is referred to as Ku and the oscillation period is referred to as Tu.
For a P controller: set Kp to 0.5Ku
For a PI controller: Kp = 0.45Ku, Ki = 1.2Kp/Tu
For a PID controller: Kp = 0.6Ku, Ki = 2Kp/Tu, Kd = KpTu/8

These can be used as starting points and then fine tuning can be performed as needed for the particular system of interest.

Things like integrals and derivatives assume continuous time. In practice, though, we are often sampling values from an ADC or something similar. This leads us to a discrete-time equivalent: the PSD controller (proportional, sum, difference), as summation is the equivalent of integration, and a difference is equivalent to a derivative.

##Arduino Example /******************************************************** * PID Basic Example * Reading analog input 0 to control analog PWM output 3 ********************************************************/

#include <PID_v1.h>

//Define Variables we'll be connecting to
double Setpoint, Input, Output;

//Specify the links and initial tuning parameters
PID myPID(&Input, &Output, &Setpoint,2,5,1, DIRECT);

void setup()
{
  //initialize the variables we're linked to
  Input = analogRead(0);
  Setpoint = 100;

  //turn the PID on
  myPID.SetMode(AUTOMATIC);
}

void loop()
{
  Input = analogRead(0);
  myPID.Compute();
  analogWrite(3,Output);
}

##References PID Controller (Wikipedia) - Overview of PID Control
Arduino PID Library - Library of Arduino PID code with many useful functions. Also includes code examples