Introduction to Recursion

Imagine you have to build a robot which can perform a certain task, like add A to B, now you are told to use a unit from an infinite supply of units which can only add and subtract 1 to/from a number provided to it, and also perform logical operations. How will you build a system which adds A to B perfectly.

You'll give both number to the robot, which will pass them to a secondary robot which adds 1 to A and subtract 1 from B and keep passing along until B is 0, and then the final value is returned. Here we don't violate the rules and still get an answer.

With recursion you can breakdown a complex problem into a simpler unit which can be solved by calling the same function again and again till a certain stop condition is reached

int add(int a,int b)
{
	if(b==0)		  //By the time b becomes 0, a becomes a+b
	    return a;             //As a is now a+b it is safe to return the new value
	return add(a+1,b-1);	  //Here the output of the secondary call is returned from primary call
}			          //which also applies for that secondary call and further ahead.

Recursion is a technique by which a function repeatedly calls itself (Or a different function) to have a effect similar to a loop.

A Recursive function in it's most basic form consists of two parts.

• Base case
• Recursive call This flow chart shows how a basic recursive function works

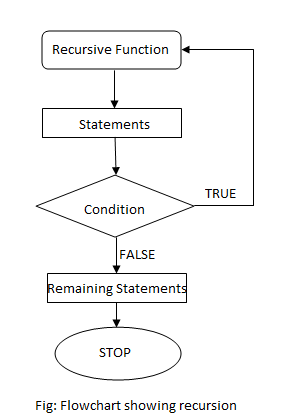
Base Case

The base case or the terminal case consists of the final step of the function which marks the end of the recursive calls.

Recursive call

This step usually performs the calculations required and calls a smaller version of the main problem. This goes on until it reaches the base case.

Choosing base case and recursive call

The choice of the base case and recursive call for your function is really important as these decide how your function works

The recursive call of your function must be such that at each successive recursive call the function reaches closer to your base case, i.e. after multiple calls to your function, you should eventually reach your base case.

The base case of your function decides when your function ends, so your base case should be selected such that your recursive case can never overshoot your base case.

Examples

Example 1 : Fibonacci series

The Fibonacci series in mathematics is represented by F(0) = 1, F(1) = 1, F(x) = F(x-1) + F(x-2) This problem gives us the perfect example of where to use recursion This code in c++ would be

int fibonacci(int x)
{
	if(x == 0 || x == 1)
	    return 1;
        return fibonacci(x - 1) + fibonacci(x - 2);
}

The same code in Python would be

def fibonacci(x):
	if x == 0 or x == 1:
		return 1
	return fibonacci(x - 1) + fibonacci(x - 2)

and in Java

public int fibonacciRecursion(int n)
{
	if(n == 0)
		return 0;
	if(n == 1 || n == 2)
		return 1;
	return fibonacciRecursion(n-2) + fibonacciRecursion(n-1);
}

Here if(x == 0 || x == 1) is the base case and it returns when x = 0 or x = 1 and return fibonacci(x-1) + fibonacci(x-2) is the recursive call. We can verify that the recursive call can never go below 1 or 0 as long as the initial input is valid because it is taken care of by the base case thus we never go past the base case. Also we see that with every call to the function, x is getting smaller and thus closer to the base case of 0 or 1.

Example 2 : Factorial

The factorial of a number n is F(n)=n*(n-1)*(n-2)*...*1 Code in c++ would be

int factorial(int x)
{
    if(x <= 1)
	return 1;
    return x*factorial(x - 1);
}

Similarly in python this code becomes

def factorial(x):
    if x <= 1:
	return 1
    return x*factorial(x - 1)

and in Java

public int factorial(int n)
{    
	if (n == 0)    
		return 1;    
	else    
		return(n * factorial(n-1));    
}

Again here if(x==1) is the base case and returns when x is 1 and x*factorial(x - 1) is the recursive call. Here too we see that x can never go below 1 as long as the initial input is above 1 and we also notice that with every successive recursive call, x gets closer to 1.

Additional Reference: Recursion Playlist