Binary Search - AryamannNingombam/IECSE-Code-Spring-2022 GitHub Wiki

Introduction to Binary Search

A general method for searching for an element in an array is to use a for loop that iterates through the elements of the array. For example, the following code searches for an element x in an array:

for (int i = 0; i < n; i++)
{
    if (array[i] == x)
    {
        // x found at index i
    }
}

The time complexity of this approach is O(n), because in the worst case, it is necessary to check all elements of the array. If the order of the elements is arbitrary, this is also the best possible approach, because there is no additional information available where in the array we should search for the element x.
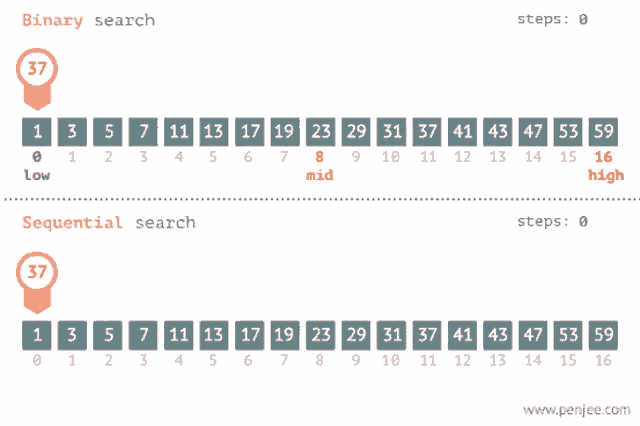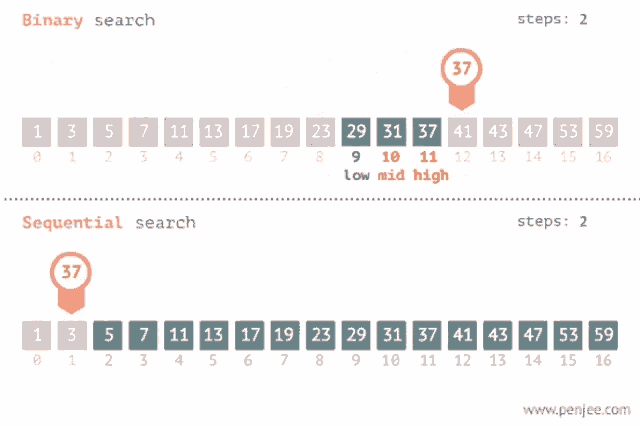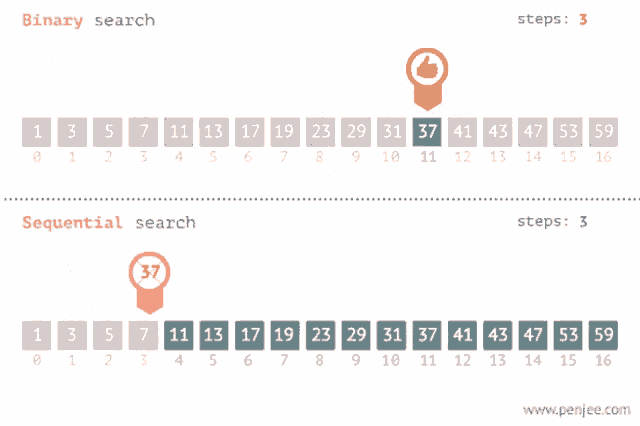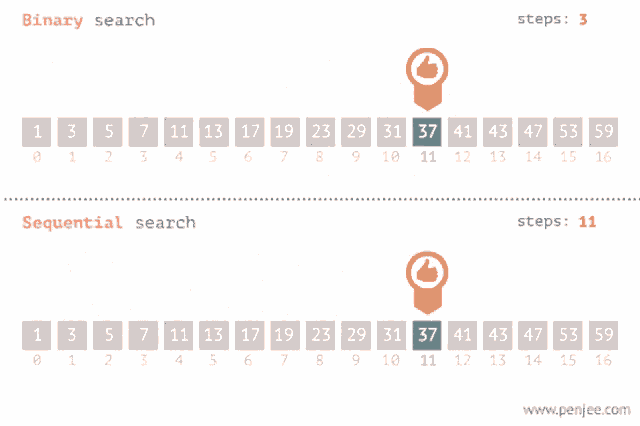
However, if the array is sorted, the situation is different. In this case it is possible to perform the search much faster, because the order of the elements in the array guides the search. The following binary search algorithm efficiently searches for an element in a sorted array in O(log n) time.
The search maintains an active region in the array, which initially contains all array elements. Then, a number of steps is performed, each of which halves the size of the region. At each step, the search checks the middle element of the active region. If the middle element is the target element, the search terminates. Otherwise, the search recursively continues to the left or right half of the region, depending on the value of the middle element.

int a = 0, b = n-1;
while (a <= b) {
    int k = (a+b)/2;    // better way: k = a+(b-a)/2
    if (array[k] == x) {
        // x found at index k
    }
    if (array[k] > x) b = k-1;
    else a = k+1;
}

In this implementation, the active region is a...b, and initially the region is 0...nāˆ’1. The algorithm halves the size of the region at each step, so the time complexity is O(log n).

Binary Search GIF

Recursive implementation of Binary Search:

// A recursive binary search function. It returns
// location of x in given array arr[l..r] is present,
// otherwise -1
int binarySearch(int arr[], int l, int r, int x)
{
    if (r >= l) {
        int mid = l + (r - l) / 2;
  
        // If the element is present at the middle
        // itself
        if (arr[mid] == x)
            return mid;
  
        // If element is smaller than mid, then
        // it can only be present in left subarray
        if (arr[mid] > x)
            return binarySearch(arr, l, mid - 1, x);
  
        // Else the element can only be present
        // in right subarray
        return binarySearch(arr, mid + 1, r, x);
    }
  
    // We reach here when element is not
    // present in array
    return -1;
}

Formula for middle index

To find the middle index of an array we usually use the following formula:

int mid = (low + high)/2;

However, the preferable formula to use is:

int mid = low + (high ā€“ low)/2;

The reason for this is that the former formula fails if the sum of low and high is greater than the maximum positive int value( 231 ā€“ 1 ). The sum overflows to a negative value and the value stays negative when divided by 2. In java, it throws ArrayIndexOutOfBoundException.

Lower Bound and Upper Bound Functions

The lower_bound() method in C++ is used to return an iterator pointing to the first element in the range [first, last) which has a value not less than val. This means that the function returns the index of the next smallest number just greater than or equal to that number. If there are multiple values that are equal to val, lower_bound() returns the index of the first such value.
Similarly, the upper_bound() method in C++ is used to return an iterator pointing to the first element in the range [first, last) which has a value higher than val. Returns pointer to the position of next higher number than val if container does not contain occurrence of val.

Use of built-in lower_bound() and upper_bound() functions in STL

Demonstration of how it works:

#include <bits/stdc++.h>
using namespace std;
// Function to implement lower_bound
int lower_bound(int arr[], int N, int X)
{
	int mid;

	// Initialise starting index and
	// ending index
	int low = 0;
	int high = N;

	// Till low is less than high
	while (low < high) {
		mid = low + (high - low) / 2;

		// If X is less than or equal
		// to arr[mid], then find in
		// left subarray
		if (X <= arr[mid]) {
			high = mid;
		}

		// If X is greater arr[mid]
		// then find in right subarray
		else {
			low = mid + 1;
		}
	}

	// if X is greater than arr[n-1]
	if(low < N && arr[low] < X) {
	low++;
	}
	
	// Return the lower_bound index
	return low;
}

// Function to implement upper_bound
int upper_bound(int arr[], int N, int X)
{
	int mid;

	// Initialise starting index and
	// ending index
	int low = 0;
	int high = N;

	// Till low is less than high
	while (low < high) {
		// Find the middle index
		mid = low + (high - low) / 2;

		// If X is greater than or equal
		// to arr[mid] then find
		// in right subarray
		if (X >= arr[mid]) {
			low = mid + 1;
		}

		// If X is less than arr[mid]
		// then find in left subarray
		else {
			high = mid;
		}
	}

	// if X is greater than arr[n-1]
	if(low < N && arr[low] <= X) {
	low++;
	}

	// Return the upper_bound index
	return low;
}

// Function to implement lower_bound
// and upper_bound of X
void printBound(int arr[], int N, int X)
{
	int idx;
		// Find lower_bound
		idx = lower_bound(arr, N, X);
		cout<<"Lower bound of "<<X<<" is "<<arr[idx]<<" at index "<<idx<<endl;

		// Find upper_bound
		idx = upper_bound(arr, N, X);
		cout<<"Upper bound of "<<X<<" is "<<arr[idx]<<" at index "<<idx<<endl;
}

// Driver Code
int main()
{
	// Given array
	int arr[] = { 4, 6, 10, 12, 18, 20 };
	int N = sizeof(arr) / sizeof(arr[0]);

	// Element whose lower bound and
	// upper bound to be found
	int X = 6;

	// Function Call
	printBound(arr, N, X);
	return 0;
}
āš ļø **GitHub.com Fallback** āš ļø