A graph is a set of vertices connected by zero or more edge.

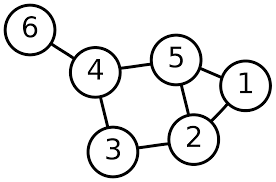
• weight - "weight" of an edge. can also be interpreted as the length of an edge.
• un / weighted graph - term where the edge of a graph has / does not have weight.
• un / directed edge - term to say if an edge is bidirectional / one-way.
• path - a sequence of one or more edges passed to link two vertices.
• connected - a graph where there is at least one path for each vertex pair.
• cycle - a path starting and ending at the same vertex without traversing the same two edges.
• tree - an undirected connected graph that does not have a cycle.
• root - vertex with the lowest depth.
• ancestor - set of vertex passed in a path from root to a vertex.
• parent - ancestor of the node that has the highest depth.
• child - set of vertex connected to an edge and not an ancestor.

There are 3 ways that are often used to represent a graph, namely

1. Adjacency Matrix
   We can represent a graph using a 2-dimensional array Adjmat [V][V] where AdjMat [i][j] is 1 if there is a edge connecting vertex i and vertex j and 0 if it doesn't exist. The value of AdjMat[i][j] can also be weight from a edge to weighted graph. For example, the adjacency matrix for the graph in the example is as follows:

0 1 0 0 1 0
1 0 1 0 1 0
0 1 0 1 0 0
0 0 1 0 1 1
1 1 0 1 0 0
0 0 0 1 0 0

2. Adjacency List
   The main problem with using an adjacency matrix is ​​that it consumes as much as $V^2$ of memory for a graph with as many vertices as $V$ so it is not possible for a large graph.
   The solution to this problem is to use the Adjacency List. The idea of ​​representing using the Adjacency List is to simply keep a list of other vertices that have an edge connected to a vertex. The implementation can be done using a vector like the following:

vector<int>adjList [V];
// insert edge a-b
adjList[a].push_back(b);
adjList[b].push_back(a);

for weighted graph we can use pair <int,int> as content of Adjacency List to store adjacent vertex and their weight. Here's an implementation for a weighted graph:

vector <pair <int,int>>adjList[V];
// inserts edge a-b with weight c
adjList[a].push_back (make_pair(b,c));
adjList[b].push_back (make_pair(a,c));

The use of this method in representing graphs is highly recommended because it is very efficient in memory usage and the time complexity of traversing.

3. Edge List
   The idea of ​​representing a graph using this method is to save all the existing lists in a graph. Storage can be done in a static or dynamic array such as vector
   The implementation can use a struct containing the vertex at the end of the edge and its weight. Another alternative if lazy creates a struct is to use a pair <pair <int,int>,int> to store the required information.
   Examples of implementation are as follows:

vector <pair<pair<int,int>,int>> edgeList;
// inserts edge a-b with weight c
edgeList.push_back(make_pair(make_pair(a, b),c));

For unweighted graph we can change the contents of the vector to pair<int,int>.
This method is very useful in the Kruskal algorithm to find the Minimum Spanning Tree of a graph
Note: even though it looks a little more complicated, I prefer the option of using pairs because actually using structs is hard.

In some cases, we don't need a special data structure to store a graph so that it can be traced or operated. These cases occur if the graph is implicit graph.

2 The general form of implicit graph, namely:

1. A graph with implicit edges
   Example 1:
   As you often encounter in recursion modules at the basics of programming, a grid that contains the character '.' or '#' where we cannot visit grids containing '#'. (Figure A)
   Unconsciously, this is a graph where the vertex is the position containing '.' with an edge connects the two '.' touching each other. (Figure B)
   It can be seen that we don't need any of the 3 techniques to represent graphs as previously described.
   Example 2:
   A graph that is formed based on the movement of the horse pawns in a chess game. We can think of the tiles on chess as vertices of the graph, as well as an edge connecting 2 tiles if the tile can be visited by performing the pawn move. (Figure C)
2. A graph with an edge that follows a rule
   Example:
   A graph with N vertices ([1..N]) where there is an edge connecting $i$ and $j$ if $(i+j)$ is prime. (Figure D)