As the name implies, DFS will traversal to the deepest vertex. Every time you arrive at a vertex $u$, DFS will select one of the vertex associated(neighbouring) with vertex $u$ that had never been visited before, then continue searching from that vertex. This step continues as long as we still find vertex that can still be visited. If it doesn't exist, it will do backtracking then return to look for vertex that can be visited. An example of implementing in a weighted graph can be done recursively like the following code:

vector <pair<int,int>> adjList[N];
bool visited[N];

void dfs(int curVertex)
{
    // marks that this vertex has already been visited
    visited[curVertex] = 1; // Look at this line for a trivia question
    for (int i = 0; i <adjList[curVertex].size(); i++) // scrolls through the list of vertices associated with curVertex
    {
        int nextVertex = adjList[curVertex][i].first;
        // note that in pairs,
        // first is the vertex number and second
        // is the weight
        if (!visited[nextVertex]) // checks if not already visited
        {
            dfs(adjList[nextVertex]);
            // do something
        }
    }
    // do something
}

Traversal using BFS starts from a vertex, then will visit the vertex which is directly connected (neighbouring) to the vertex (layer 1). Then, in the next step we will visit vertex which is directly connected to vertex - vertex on layer 1 (layer 2) and so on until there is no more vertex that can be visited. Unlike DFS, the implementation of BFS can be done iteratively by using the queue data structure as follows:

vector <int> adjList[N];
bool visited[N];

void bfs (int startNode)
{
    queue <int> q;
    q.push(startNode);
    visited[startNode] = 1;
    while (!q.empty()) // Anyone know why this is?
    {
        int curNode = q.front();
        q.pop();
        for (int i = 0; i <adj[curNode].size (); i++) // same as DFS
        {
            int nextNode = adj[curNode][i];
            if (! visited[nextNode])
            {
                q.push(nextNode);
                visited[nextNode] = 1; // Look at this line for a trivia question
            }
        }
    }
}

Trivia question: in DFS, we tag the nodes before iterating over the contents of the adjacency list, whereas in BFS, we tag them in iterations. Does the timing of the placement of these marks affect the algorithms? If so, what effect would it have?

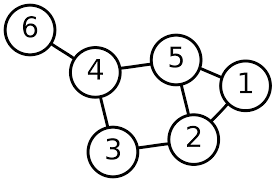
If we do BFS on the graph from vertex 1, the vertices for each layer are:

• Layer 0: 1
• Layer 1: 2 5
• Layer 2: 3 4
• Layer 3: 6

Note that the number of layers is the number of minimal edges that must be passed to get to the vertex from vertex 1 or so-called shortest path.