Module 3: AVL Tree - AlproITS/StrukturData GitHub Wiki
AVL Tree is a self-balancing BST where each node keeps a balanced height difference between its right and left children. This balanced height is called a balance factor, and the value has to be either -1, 0, or 1.
AVL tree has similar terminologies as the previous module. Some additions:
- Height: the amount of levels in a tree
- Balance Factor : the height difference between left and right sub-trees
- Ancestor: a node that is connected to all lower-level nodes; any other node on the path from a node to the root

Complete implementation of AVL Tree >
Node representation in an AVL Tree is the same as BST, only there's an additional data of height in each node.
typedef struct AVLNode_t
{
int data;
struct AVLNode_t *left,*right;
int height;
}AVLNode;
typedef struct AVL_t
{
AVLNode *_root;
unsigned int _size;
}AVL;-
To initiate an AVL Tree we can use the operations in
avl_init()void avl_init(AVL *avl) { avl->_root = NULL; avl->_size = 0u; }
-
The
heightvariable is used to get the balance factor of a nodeint _getHeight(AVLNode* node){ if(node==NULL) return 0; return node->height; }
AVL balances itself by rotating its structure until the balance factor fits the right condition (has to be either -1, 0, or 1)
There are 2 primary kinds of rotation used in an AVL Tree: Right Rotation and Left Rotation. To determine which rotation to be performed during insertion/deletion of a node, we need to iteratively get the balance factors of the right and left sub-trees.
int _getBalanceFactor(AVLNode* node){
if(node==NULL)
return 0;
return _getHeight(node->left)-_getHeight(node->right);
}There are 4 possibilities:
-
If Balance Factor > 1 / height of left subtree > height of right subtree :
- height of left subtree > height of right subtree (Case left skewed) -> Right Rotation
- height of left subtree > height of right subtree (Case left right zigzag) -> Left Rotation followed by Right Rotation
-
If Balance Factor < -1 / height of right subtree > height of left subtree :
- height of right subtree > height of left subtree (Case right skewed) -> Left Rotation
- height of right subtree > height of left subtree (Case right left zigzag) -> Right Rotation followed by Left Rotation
Two kinds of rotation: Left Rotation and Right Rotation.
-
AVLNode* _rightRotate(AVLNode* pivotNode){ AVLNode* newParrent=pivotNode->left; pivotNode->left=newParrent->right; newParrent->right=pivotNode; pivotNode->height=_max(_getHeight(pivotNode->left), _getHeight(pivotNode->right))+1; newParrent->height=_max(_getHeight(newParrent->left), _getHeight(newParrent->right))+1; return newParrent; }
pivotNodeis the current node which we set as a pivot for the rotation.Right Rotation sets the left child of pivotNode to be the new parent. Then the right child of the new parent is set to be the left child of pivotNode. pivotNode will then be the right child of the new parent. In the end, update the heights for both pivotNode and newParent nodes.
Right Rotation solves Case Left Skewed.
AVLNode* _leftCaseRotate(AVLNode* node){ return _rightRotate(node); }

-
AVLNode* _leftRotate(AVLNode* pivotNode){ AVLNode* newParrent=pivotNode->right; pivotNode->right=newParrent->left; newParrent->left=pivotNode; pivotNode->height=_max(_getHeight(pivotNode->left), _getHeight(pivotNode->right))+1; newParrent->height=_max(_getHeight(newParrent->left), _getHeight(newParrent->right))+1; return newParrent; }
Left Rotation takes the right child of pivotNode to be the new parent. The left child of newParent will become the right child of pivotNode. Then, pivotNode is set to be the right child of he new parent.
Left Rotation solves Case Right Skewed.
AVLNode* _rightCaseRotate(AVLNode* node){ return _leftRotate(node); }

-
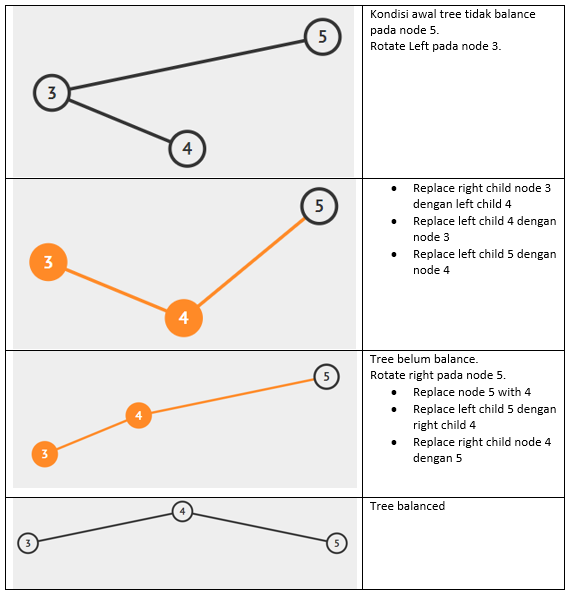
Case left right zigzag can be solved using Left Rotation followed by Right Rotation.
AVLNode* _leftRightCaseRotate(AVLNode* node){ node->left=_leftRotate(node->left); return _rightRotate(node); }
-
AVLNode* _rightLeftCaseRotate(AVLNode* node){ node->right=_rightRotate(node->right); return _leftRotate(node); }
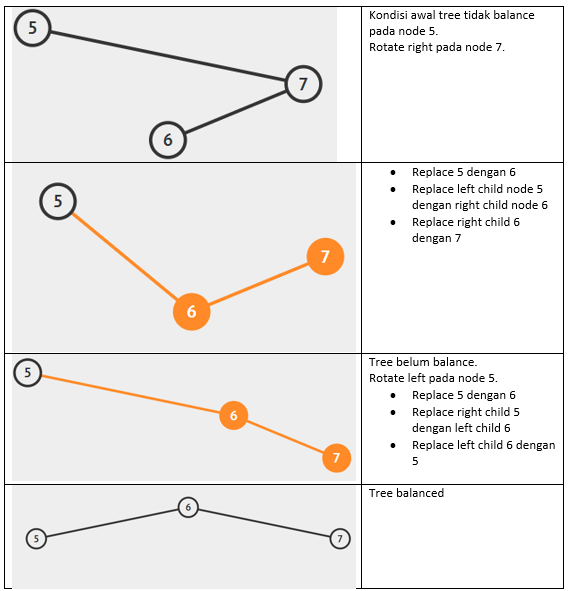
Insertion in an AVL Tree can be done by performing the standard new node insertion in BST. Then, we update the height of each new node ancestor. Leaf nodes will have the height value of 1 (to handle empty nodes easier). For every node other than the leaf nodes, the height value is equal to the maximum height between its children + 1. Then we check the balance factor of each ancestor node (height of left node - height of right node or vice versa). If any imbalanced node is found, rotation will be performed.
-
To create a new node.
AVLNode* _avl_createNode(int value) { AVLNode *newNode = (AVLNode*) malloc(sizeof(AVLNode)); newNode->data = value; newNode->height=1; newNode->left = newNode->right = NULL; return newNode; }
To search for a node with a certain value.
AVLNode* _search(AVLNode *root, int value) { while (root != NULL) { if (value < root->data) root = root->left; else if (value > root->data) root = root->right; else return root; } return root; }
To insert new data to an AVL Tree.
AVLNode* _insert_AVL(AVL *avl,AVLNode* node,int value){ if(node==NULL) return _avl_createNode(value); if(value < node->data) node->left = _insert_AVL(avl,node->left,value); else if(value > node->data) node->right = _insert_AVL(avl,node->right,value); node->height= 1 + _max(_getHeight(node->left),_getHeight(node->right)); int balanceFactor=_getBalanceFactor(node); if(balanceFactor > 1 && value < node->left->data) return _leftCaseRotate(node); if(balanceFactor > 1 && value > node->left->data) return _leftRightCaseRotate(node); if(balanceFactor < -1 && value > node->right->data) return _rightCaseRotate(node); if(balanceFactor < -1 && value < node->right->data) return _rightLeftCaseRotate(node); return node; }
-
Main function to check if a node with a certain value exists.
bool avl_find(AVL *avl, int value) { AVLNode *temp = _search(avl->_root, value); if (temp == NULL) return false; if (temp->data == value) return true; else return false; }
Main function to insert a new data.
void avl_insert(AVL *avl,int value){ if(!avl_find(avl,value)){ avl->_root = _insert_AVL(avl,avl->_root,value); avl->_size++; } }
Similar to performing insertion, deletion in AVL Tree can be performed like the usual node removal in BST. Then we update the height for all nodes, followed by balance factor checking to look for any imbalances. If any imbalanced node is found, rotation will be performed.
-
AVLNode* _findMinNode(AVLNode *node) { AVLNode *currNode = node; while (currNode && currNode->left != NULL) currNode = currNode->left; return currNode; }
AVLNode* _remove_AVL(AVLNode* node,int value){ if(node==NULL) return node; if(value > node->data) node->right=_remove_AVL(node->right,value); else if(value < node->data) node->left=_remove_AVL(node->left,value); else{ AVLNode *temp; if((node->left==NULL)||(node->right==NULL)){ temp=NULL; if(node->left==NULL) temp=node->right; else if(node->right==NULL) temp=node->left; if(temp==NULL){ temp=node; node=NULL; } else *node=*temp; free(temp); } else{ temp = _findMinNode(node->right); node->data=temp->data; node->right=_remove_AVL(node->right,temp->data); } } if(node==NULL) return node; node->height=_max(_getHeight(node->left),_getHeight(node->right))+1; int balanceFactor= _getBalanceFactor(node); if(balanceFactor>1 && _getBalanceFactor(node->left)>=0) return _leftCaseRotate(node); if(balanceFactor>1 && _getBalanceFactor(node->left)<0) return _leftRightCaseRotate(node); if(balanceFactor<-1 && _getBalanceFactor(node->right)<=0) return _rightCaseRotate(node); if(balanceFactor<-1 && _getBalanceFactor(node->right)>0) return _rightLeftCaseRotate(node); return node; }
-
void avl_remove(AVL *avl,int value) { if(avl_find(avl,value)) { avl->_root=_remove_AVL(avl->_root,value); avl->_size--; } }
