Sesuai dengan namanya, DFS akan melakukan traversal sampai ke vertex yang paling 'dalam'. Setiap kali sampai di suatu vertex $u$, DFS akan memilih salah satu vertex yang terhubung dengan vertex $u$ dan belum pernah dikunjungi sebelumnya, lalu melanjutkan penelusuran dari vertex tersebut. Langkah ini terus dilakukan selama kita masih menemukan vertex yang masih bisa dikunjungi. Jika sudah tidak ada, akan dilakukan backtracking lalu kembali mencari vertex yang bisa dikunjungi.
Contoh pengimplementasian dalam weighted graf dapat dilakukan secara rekursif seperti kode berikut:

vector<pair<int,int>> adjList[N];
bool visited[N];

void dfs(int curVertex)
{
    //menandai bahwa vertex ini sudah pernah dikunjungi
    visited[curVertex] = 1; //Perhatikan baris ini untuk trivia question
    for (int i = 0 ; i < adjList[curVertex].size() ; i++) //menelusuri daftar vertex yang terhubung dengan curVertex
    {
        int nextVertex = adjList[curVertex][i].first;
        //perhatikan bahwa dalam pair,
        // first merupakan nomor vertex serta second
        //merupakan weightnya
        if (!visited[nextVertex]) //mengecek jika belum dikunjungi
        {
            dfs(adjList[nextVertex]);
            //do something
        }
    }
    //do something
}

Traversal menggunakan BFS dimulai dari sebuah vertex, lalu akan mengunjungi vertex yang terhubung langsung dengan vertex tersebut (layer 1). Lalu, di langkah selanjutnya akan mengunjungi vertex yang terhubung langsung dengan vertex - vertex pada layer 1 (layer 2) dan seterusnya sampai sudah tidak ada lagi vertex yang bisa dikunjungi.
Berbeda dengan DFS, pengimplementasian BFS dapat dilakukan secara iteratif dengan menggunakan bantuan queue seperti berikut :

vector<int> adjList[N];
bool visited[N];

void bfs(int startNode)
{
    queue<int> q;
    q.push(startNode);
    visited[startNode] = 1;
    while (!q.empty()) // ada yang tau kenapa seperti ini?
    {
        int curNode = q.front();
        q.pop();
        for (int i = 0 ; i < adj[curNode].size() ; i++) // sama seperti DFS
        {
            int nextNode = adj[curNode][i];
            if (!visited[nextNode])
            {
                q.push(nextNode);
                visited[nextNode] = 1; //Perhatikan baris ini untuk trivia question
            }
        }
    }
}

Trivia question : pada DFS, kita melakukan penandaan pada node sebelum mengiterasi isi dari adjacency list, sedangkan pada BFS, kita melakukan penandaan di dalam iterasi. Apakah timing penempatan tanda ini berpengaruh pada algoritma-algoritma tersebut? Jika iya, apa pengaruhnya?

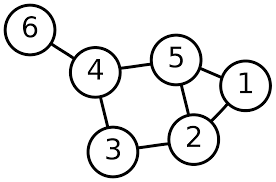
Jika kita melakukan BFS pada graf tersebut dari vertex 1, maka vertex-vertex tiap layer adalah:

• Layer 0 : 1
• Layer 1 : 2 5
• Layer 2 : 3 4
• Layer 3 : 6

Perhatikan bahwa jumlah layer adalah jumlah dari edge minimal yang harus dilewati untuk sampai ke vertex tersebut dari vertex 1 atau biasa disebut dengan shortest path.