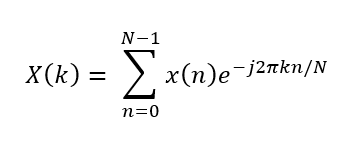The Fast Fourier Transform and Its Applications - 180D-FW-2023/Knowledge-Base-Wiki GitHub Wiki
Introduction
Word Count: 2,245
Our existence in this universe is entirely governed by the reception of stimuli; whether it be the shade of a certain color, a musical note, or the vibration from a passing car our experiences and perceptions rest on sensory input. Thus, the study of signal processing, a field concerned with analyzing any function that delivers information, is an indispensable and uniquely important aspect of Electrical Engineering. The extent to which signal processing applies to the operation of everyday life in the modern world has garnered it the status as the crown jewel of engineering; within this field, the single most crucial concept is the fast Fourier transform algorithm.
The FFT and Its History
The Fourier Transform
While we are most comfortable investigating information within the time domain, it is possible and extremely useful to perform our analysis through the lens of the frequency domain. Rather than characterizing a signal through its temporal behavior, a signal can be decomposed into a collection of independent sine and cosine functions. In particular, we can leverage complex exponentials, which are equivalent to the superposition of a real cosine and imaginary sine wave by Euler's identity, as a basis to convert mathematical computations into the realm of frequencies. The Fourier transform is the primary tool utilized to carry out this conversion.
Figure 1: Fourier transform analysis and synthesis equations
As presented in the figure above, the Fourier transform is an integral formula that determines the presence of frequencies in a signal by calculating their "weight" through a summation of the product of a complex exponential of the respective frequency and the signal of interest. In essence, the Fourier transform converts information into a circular framework, which is achieved by the complex exponential component, and identifies the strength of specific frequencies by calculating their center of mass within the framework, a process executed by the integration.

Figure 2: Visual representation of Fourier transform for an elementary signal
The Discrete Fourier Transform
A significant portion of the signals that we encounter are not continuous but discrete. The resolution of information we can extract from the signal is dependent on the number of samples present. Similar to the continuous analog case above, there exists a Fourier transform for discrete information. However, the maximum number of frequencies that can be detected is limited by the total samples. The frequency profile generated by the discrete Fourier transform is divided into bins, whereby bins are classified as integer multiples of a fundamental frequency inversely proportional to the total duration of the signal. Moreover, a maximum frequency measurable exists and is determined by the spacing of the samples.

Figure 3 & 4: Discrete Fourier transform analysis formula and visualization of DFT on a discrete signal
The discrete Fourier transform in Figure 3 closely resembles the continuous form, the only difference being that the summation is finite as there are a limited number of samples. Likewise, Figure 4 illustrates the discrete division of the signal's frequencies into bins of a nonzero width.
The FFT and early applications
The Fourier transform is named after French Mathematician Jean-Baptiste Joseph Fourier, who devised the key insight of translating functions into expanded trigonometric series through the study of the propagation of heat through solid bodies. The significance of Fourier's insight bloomed as tools for signal processing became more sophisticated. The watershed moment for the Fourier Transform occurred in 1965 when the world's circumstances necessitated the creation of a more efficient algorithm, ultimately resulting in the invention of the Fast Fourier Transform. Post World War II, nations overzealously entered a nuclear arms race and quickly thereafter strived to ban atomic bomb tests. The greatest challenge faced by the world's leading scientists was discovering whether nuclear weapons were being detonated underground. This information could be derived from seismograph readings through a Fourier transform; the frequency profile extracted from a detonation could discriminate it from other seismic activity and provide information such as the testing depth and the explosion power. However, the number of computations required to complete the traditional transformation was much too intense for the technology at the time and would take years to complete. Inspecting the formula in Figure 3, one can see that for a total of N samples, each sample will require N computations for the transformation, resulting in a total complexity of O(N^2); this order of complexity is not friendly for performing calculations spanning a large number of samples as it scales at an alarming rate. To accelerate the process of detecting nuclear tests, two scientists, James Cooley and John Tukey, created a faster algorithm for completing the transformation by identifying the presence of duplicate information within their calculations. Specifically, a symmetry exists between the values of the complex exponential at the sample locations due to periodicity. The data can be divided into even and odd points, and one can observe that for a given sinusoidal harmonic k its mirror harmonic N+k will expose a symmetry aligned at the even points and an anti-symmetry aligned at the odd points. As a result, the total required computations can be split in half. This reduction can be leveraged recursively for the even and odd components culminating in a "divide and conquer" approach with an O(Nlog(N)) complexity, the basis of the fast Fourier transform algorithm. The speed of an O(Nlog(N)) process compared to that of an O(N^2) is remarkable and allows for the computation of large data sets within a reasonable amount of time.

Figure 5: Diagram visually highlighting the recursive binary division of computations in a fast Fourier Transform
Compression
The genesis of the fast Fourier transform occurred through the analysis of seismograph readings. However, the power of the FFT algorithm is ubiquitous in signal processing and is critical in a wide variety of applications. One such application is that of compression, specifically image compression. Much of the data stored on modern machines is derived from digital images. In their raw form, digital images are expensive in terms of their cost of memory storage, and the fast Fourier transform plays a pivotal role in reducing this burden. A given digital image can be decomposed into individual pixels, where each pixel represents a single sample point. A fast Fourier transform can then be applied to the collection of pixels, where the number of frequencies extracted from the image is equivalent to the total number of pixels. An image is a two-dimensional object, meaning the operation applied is a two-dimensional fast Fourier transform; although this computation may seem complicated in higher dimensions, it is simply performed by transforming every row of the image and then transforming every column of the new image. Following this process, one can observe that in almost all images a vast majority of the Fourier coefficients have a near-negligible magnitude, meaning that the frequencies associated with those coefficients are barely visible in the image and can be considered excess information that increases storage cost. Therefore, one can assign a null value to these frequencies and focus on only storing information relating to the noticeable frequencies, which only consist of a small fraction of the total data profile. The total energy within the time domain and frequency domain is related by Parseval's theorem.
Figure 6: Parseval's theorem
Parrseval's theorem dictates that because only a tiny amount of energy is lost when the negligible frequency coefficients are disregarded, only a tiny amount of energy is lost in the time domain as well; when an inverse fast Fourier transform is performed on the filtered frequency domain image, the resulting image will be nearly identical to the original with minimal loss in quality. Therefore it is possible to store and recreate a given digital image using only a fraction of the data present through the employment and manipulation of a fast Fourier transform. This serves as the core of the JPEG storage format, and the high-level process of all image compression follows 5 main steps:
- Implement and compute the fast Fourier transform of an image to translate data into the frequency domain
- Normalize the FFT data set by shifting the DC offset to the center of the frequency spectrum
- Apply thresholding by leveraging different filter types (Butterworth, Gaussian, Chebyshev) to create a bandpass that isolates visible frequencies
- Invert step 2 by decentralizing the data set and moving the DC offset to its original position
- Perform inverse fast Fourier transform to recover the image back from the frequency domain
Figure 7: 2-Dimensional FFT and filtered FFT of an image. Observe that in the magnitude spectrum, only the points near the center are distinguishable, and the inverted image from the filtered case closely resembles the original image
More Sophisticated Applications of the FFT for Compression
Naturally, a desirable goal for a system engineer is discovering a method to apply the FFT and maximize data compression while minimizing loss in resolution. This goal requires investigating techniques more complex than the standard FFT algorithm, as the optimal filtering in the compression process is unique to any individual image/data set. One such technique is the adoption of the Intelligent Water Drop algorithm, a mathematical concept arising from graph theory that addresses the Travelling Salesman Problem. The IWD algorithm studies the behavior of water drops flowing from elevated to low-altitude areas and is used as a tool in discrete mathematics to identify the probability of node transitions in a graph under certain conditions. This algorithm can be applied to the fast transform to optimize the thresholding process; the IWD algorithm aids in estimating the RGB values for a given threshold filter to maximize the filter's compression ratio and its structural similarity index, a parameter indicating the resemblance of one image to another.
The FFT Figure 8: Reconstruction of an image using different threshold values for the IFFT
Utilizing this hyper-efficient modification of the FFT, technology such as Medical Imaging systems can be improved and accelerate treatment and diagnosis in the health sector. In the medical field, it is critical to possess detailed images of patients to successfully perform surgeries and other operations, though the sheer number of recorded images warrants the use of compression. Along with the IWD algorithm previously discussed, biomedical engineers propose additional stages to the traditional compression process to refine medical imaging. The main proposal is the implementation of Entropy encoding or Huffman encoding to achieve near-lossless compression. This encoding revolves around the concept of identifying patterns within a data set and assigning varying weights to these patterns based on how frequently they occur. Integrating this technique with the FFT and hardware such as FPGAs enables healthcare workers to efficiently process and analyze Medical Images.
Figure 9: PET scan realized through an involved FFT procedure
Additional Applications of the FFT
Radio Astronomy
The discussion above has revolved around performing the FFT on signals in the visual spectrum. However, the FFT can provide a frequency profile for any general signal, including those belonging to the radio category. As a result, the FFT is incredibly helpful in astronomical studies where spectroscopy is a primary method of identifying and classifying celestial bodies. The investigation of pulsars, rotating neutron stars, warrants the employment of Fourier analysis. Telescopes operating in the radio frequency are utilized to detect interstellar signals, and the FFT allows astronomers to construct and recognize the electromagnetic signature of pulsars. Additionally, the data extracted from the Fourier analysis of a pulsar delivers information such as the harmonic frequencies and the spin period of the body. A pulsar produces a large stream of electromagnetic radiation through the movement of charged particles along its magnetic pole; the resulting signals propagate through space, become entangled with background radio noise, and are redshifted before reaching Earth's surface, requiring sophisticated tools to accurately discriminate the data of interest. The FFT is one such tool and assists astronomers in working with vast amounts of data in their search for pulsars. When inspecting the frequency profile of a pulsar, one can notice large spikes correlating to the fundamental spin frequency of the star and its harmonics; this pattern can be made quickly visible through the FFT and serves as an easily identifiable signature for the presence of a pulsar. Unfortunately, these peaks often originate from vast distances and are obscured by background radiation. Interestingly, astronomers utilize the phase data in the FFT to circumvent this issue. The time series data for a pulsar signal is "folded" in a manner such that the signal is divided into equally spaced bins equivalent to the pulsar spin period and then integrated together and fast Fourier transformed to establish a signal containing the complete harmonic structure of the pulsar. This folding process is accomplished by evaluating the phase bin data in an FFT and determining the appropriate segment length to divide the signal into and superimpose together. The frequency profile of the pulsar reveals key quantities such as the pulsar's angular velocity and energy generation rate.
Figures 10 & 11: Folding and FFT of pulsar signal data and pulsar spin rate revealed through an FFT representation
General RF Applications
In continuation to the radio frequency application discussed above, the FFT is also involved in communication systems. The primary function of the FFT is to quickly provide a frequency spectrum of a given signal, and for a radio signal, this information allows engineers to detect interference from outside sources and distribute channels to relayed radio messages. The FFT's ability to facilitate signal thresholding assists engineers in designing analog and digital filters for radio circuits. Additionally, the FFT presents an elegant manner to perform signal modulation and demodulation through the analysis of a signal's frequency components. Particularly, the modulation index, or the amplitude ratio of a modulated signal to a carrier signal, can be obtained through an FFT. One can utilize an oscilloscope along with software that performs Fourier transforms to segregate a modulated signal into separate constituents, including the carrier signal/frequency. The FFT also lies at the heart of wireless communication. Orthogonal frequency division multiplexing enables modern Wi-Fi's extraordinarily quick operation by packaging subcarrier signals in an orthogonal arrangement such that they cannot interfere with one another; this process is made possible by the FFT as it deconstructs information into independent sine and cosine waves, which serve as an orthogonal basis. Antenna design for wireless systems is similarly dictated by the FFT. A Fourier transform allows engineers to analyze the radiation pattern of a given antenna and provides guidance regarding constructing an antenna to satisfy given directional characteristics.
Figure 12: FFT of an AM modulated signal on an oscilloscope, revealing the carrier signal and sideband signals
Conclusion
The fast Fourier transform is often regarded as the most important algorithm ever invented; the ingenuity of its derivation combined with its utility has granted it the status of an irreplaceable staple in applied sciences. The algorithm's application spans countless fields of interest and continues to spearhead proposed solutions to complicated engineering problems. It would be nearly impossible to traverse the modern world without encountering a piece of technology harnessing the fast Fourier Transform, which inextricably ties its importance to humanity's natural dependence on sensory input and guarantees it eternal relevance.
References
[3]. https://www.cs.cmu.edu/afs/andrew/scs/cs/15-463/2001/pub/www/notes/fourier/fourier.pdf
[4]. https://lpsa.swarthmore.edu/Fourier/Xforms/FXformIntro.html
[5]. https://databookuw.com/databook.pdf
[6]. https://www.dspguide.com/ch27/6.htm
[7]. https://www.ripublication.com/ijaer18/ijaerv13n6_54.pdf
[9]. https://resources.pcb.cadence.com/blog/2023-fast-fourier-transform-fundamentals
[10]. https://www.jsr.org/hs/index.php/path/article/download/1467/706/8164
[11]. https://resources.pcb.cadence.com/blog/2023-fast-fourier-transform-fundamentals