SymPy vs. Magma - sympy/sympy GitHub Wiki
 vs.
vs. 
SymPy and Magma are Computer algebra systems.
- Computer Algebra System
-
A software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.
SymPy is a Python library for symbolic computation that aims to become a full-featured computer algebra system and to keep the code simple to promote extensibility and comprehensibility.
SymPy was started by Ondřej Čertík in 2005 and he wrote some code in 2006 as well. In 11 March 2007, SymPy was realeased to the public. The latest stable release of SymPy is 1.0 (March 3, 2016). As of beginning of December 2001 there have been over 150 people who contributed at least one commit to SymPy.
SymPy can be used:
- Inside Python, as a library
- As an interactive command line, using IPython
SymPy is entirely written in Python and does not require any external libraries, but various programs that can extend its capabilites can be installed:
- gmpy, Cython --> speed improvement
- Pyglet, Matplotlib --> 2d and 3d plotting
- IPython --> interactive sessions
SymPy is available online at SymPy Live. The site was developed specifically for SymPy. It is a simple web shell that looks similar to the isympy console under the standard Python interpreter. SymPy Live uses Google App Engine as computational backend.
+ +: small library, pure Python, very functional, extensible, large community.
- -: slow, needs better documentation.
Magma is a computer algebra system designed to solve problems in algebra, number teory, geometry and combinatorics. It is named after the algebraic structure magma. It runs on Unix-like and Linux based operating systems, as well as Windows.
Magma was created and developed by the Computational Algebra Group within the School of Mathematics and Statistics at the University of Sidney. The development of Magma began in 1990 and the first public release was three years later, in August 1993 (version 1.0). The latest stable release is Magma V2.18-2 (16 December 2011).
Magma covers the following mathematical areas:
- Group theory
- Number theory
- Algebraic number theory
- Module theory and Linear algebra
- Sparse matrices
- Lattices and the LLL algorithm
- Commutative algebra and Gröbner bases
- Representation theory
- Invariant theory
- Lie theory
- Algebraic geometry
- Aritmetic geometry
Magma is proprietary software restricted by both trade secret and copyright law. You can try the last version of Magma (V2.18-2) online at its official site in the Calculator section. However, you must pay $1,150 if you would like to use Magma for calculations longer than 60 seconds.
+ +: fast, very functional.
- -: not open source (proprietary), expensive, doesn't have a full scientific stack.
SymPy is a cost free open source CAS released under a modified BSD license, while Magma is proprietary software, released under cost recovery (non-commercial proprietary) type of license.
| System | Windows | Mac OS X | Linux | BSD | Solaris |
|
|
|
|
|
Yes |
|
|
|
|
|
|
Yes |
|
|
Sympy is distributed in various forms. It is possible to download source tarballs and packages from the Google Code page but it is also possible to clone the main Git repository or browse the code online. The only prerequisite is Python since Sympy is Python-based library. It is recommended to install IPython as well, for a better experience.
You can order Magma from its official site. There are several versions of ordering: institution, student and special offers. While Magma is a non-commercial system, the developers are required to recover all costs arising from its distribution and support.
| System |
Formula editor |
|
|
|
|
|
|
|
|
|
|
|
|
|
| System + |
|
Graph theory |
Number theory |
Quantifier elimination |
Boolean algebra |
Tensors |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* Will be available in SymPy 0.7.2
In SymPy, to raise something to a power, you must use **, not ^ as the latter uses the Python meaning, which is xor.
In [1]: (x+1)^2
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
/home/aoi_hana/sympy/<ipython-input-6-52730bce1577> in <module>()
----> 1 (x+1)^2
TypeError: unsupported operand type(s) for ^: 'Add' and 'int'
In [2]: (x+1)**2
Out[2]:
2
(x + 1)However, in Magma, you must use ^ for exponentiation, as ** isn't defined as an operator:
> (x+1)**2;
>> (x+1)**2;
^
User error: bad syntax
> x := 2;
> (x+1)^2;
9In both SymPy and Magma you have to define symbols before you can use them.
SymPy
>>> x**2 + 2*x + 1
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
NameError: name 'x' is not defined
>>> from sympy import Symbol
>>> x = Symbol('x')
>>> x**2 + 2*x + 1
x**2 + 2*x + 1Magma
> x^2 + 2*x + 1;
>> x^2 + 2*x + 1;
^
User error: Identifier 'x' has not been declared or assignedSymPy
To perform partial fraction decomposition apart(expr, x) must be used. To combine expressions, together(expr, x) is what you need. Here are some examples of these two and other common functions in iSymPy:
In [8]: 1/( (x**2+2*x+1)*(x**2-1) )
Out[8]:
1
───────────────────────
⎛ 2 ⎞ ⎛ 2 ⎞
⎝x - 1⎠⋅⎝x + 2⋅x + 1⎠
In [9]: apart(1/( (x**2+2*x+1)*(x**2-1) ), x)
Out[9]:
1 1 1 1
- ───────── - ────────── - ────────── + ─────────
8⋅(x + 1) 2 3 8⋅(x - 1)
4⋅(x + 1) 2⋅(x + 1)
In [10]: together(1/(x**2+2*x) - 3/(x+y) + 1/(x+y+z))
Out[10]:
x⋅(x + 2)⋅(x + y) - 3⋅x⋅(x + 2)⋅(x + y + z) + (x + y)⋅(x + y + z)
─────────────────────────────────────────────────────────────────
x⋅(x + 2)⋅(x + y)⋅(x + y + z)The evalf() method and the N() function can be used to evaluate expressions:
In [20]: pi.evalf()
Out[20]: 3.14159265358979
In [23]: N(sqrt(2)*pi, 50)
Out[23]: 4.4428829381583662470158809900606936986146216893757Integrals can be used like regular expressions and support arbitrary precision:
In [24]: Integral(x**(-2*x), (x, 0, oo)).evalf(20)
Out[24]: 2.0784499818221828310Magma
The following examples show the basic usage of the eval keyword.
> x := eval "2^10";
> x;
1024Note that the expression to evaluate must be a string:
> x := eval 2^10;
>> x := eval 2^10;
^
Runtime error: Argument to eval must be a stringPartialFractionDecomposition(f) : FldFunRatUElt -> [ <RngUPolElt, RngIntElt, RngUPolElt> ] returns the unique complete partial fraction deomposition of f.
> F<t> := FunctionField(RationalField());
> f := ((t + 1)^8 - 1) / ((t^3 - 1)*(t + 1)^2*(t^2 - 4)^2);
> D := PartialFractionDecomposition(f);
> D;
[
<$.1 - 2, 1, -3683/2646>,
<$.1 - 2, 2, 410/63>,
<$.1 - 1, 1, 85/36>,
<$.1 + 1, 1, 1/108>,
<$.1 + 1, 2, 1/18>,
<$.1 + 2, 1, 1/18>,
<$.1^2 + $.1 + 1, 1, -5/147*$.1 - 8/147>
]
> F<t> := FunctionField(RationalField());
> f := (1/((t^2+2*t+1)*(t^2-1)));
> D := PartialFractionDecomposition(f);
> D;
[
<$.1 - 1, 1, 1/8>,
<$.1 + 1, 1, -1/8>,
<$.1 + 1, 2, -1/4>,
<$.1 + 1, 3, -1/2>
]SymPy
Limits in SymPy have the following syntax: limit(function, variable, point). Here are some examples:
Limit of f(x)= sin(x)/x as x -> 0
In [20]: from sympy import *
In [21]: x = Symbol('x')
In [22]: limit(sin(x)/x, x, 0)
Out[22]: 1 Limit of f(x)= 2*x+1 as x -> 5/2
In [24]: limit(2*x+1, x, S(5)/2) # The *S()* method must be used for 5/2 to be Rational in SymPy
Out[24]: 6You can also compute the left and right limits of an expression with the dir="+/-" argument.
In [5]: limit(1/x, x, oo)
Out[5]: 0
In [6]: limit(1/x, x, 0, dir="+")
Out[6]: ∞
In [7]: limit(1/x, x, 0, dir="-")
Out[7]: -∞Magma
Magma doesn't have support for limits.
SymPy
In [1]: from sympy import *
In [2]: x = Symbol('x')
In [3]: diff(cos(x**3), x)
Out[3]:
2 ⎛ 3⎞
-3⋅x ⋅sin⎝x ⎠
In [4]: diff(atan(2*x), x)
Out[4]:
2
────────
2
4⋅x + 1
In [6]: diff(1/tan(x), x)
Out[6]:
2
- tan (x) - 1
─────────────
2
tan (x)This is how you create a Bessel function of the first kind object and differentiate it:
In [7]: from sympy import besselj, jn
In [8]: from sympy.abc import z, n
In [9]: b = besselj(n, z)
In [10]: # Differentiate it:
In [11]: b.diff(z)
Out[11]:
besselj(n - 1, z) besselj(n + 1, z)
───────────────── - ─────────────────
2 2 Magma
Derivative(s) : RngDiffElt -> RngDiffElt is the image of s under the derivation of the parent of s. Notice that it can be different to the "usual" derivative, as it relies on the defined derivation.
> F<x> := RationalDifferentialField(Rationals());
> Derivative(x^3 + 5/x);
(3*x^4 - 5)/x^2
> S<t> := DifferentialLaurentSeriesRing(Rationals());
Derivative(8 + 5*t + 3*t^2);
5*t + 6*t^2JBessel(n, s) : FldReElt, FldReElt -> FldReElt calculates the value of the Bessel function of the first kind of half integral index n + (1/2), J(N+ (1/2)). Pari is used here.
> JBessel(3, Sqrt(5));
0.0955162690306062954127217774571SymPy
The syntax for series expansion is: .series(var, point, order):
In [27]: from sympy import *
In [28]: x = Symbol('x')
In [29]: cos(x).series(x, 0, 14)
Out[29]:
2 4 6 8 10 12
x x x x x x ⎛ 14⎞
1 - ── + ── - ─── + ───── - ─────── + ───────── + O⎝x ⎠
2 24 720 40320 3628800 479001600
In [30]: (1/cos(x**2)).series(x, 0, 14)
Out[30]:
4 8 12
x 5⋅x 61⋅x ⎛ 14⎞
1 + ── + ──── + ────── + O⎝x ⎠
2 24 720It is possible to make use of series(xcos(x), x)* by creating a wrapper around Basic.series().
In [31]: from sympy import Symbol, cos, series
In [32]: x = Symbol('x')
In [33]: series(cos(x), x)
Out[33]:
2 4
x x ⎛ 6⎞
1 - ── + ── + O⎝x ⎠
2 24 This module also implements automatic keeping track of the order of your expansion.
In [1]: from sympy import Symbol, Order
In [2]: x = Symbol('x')
In [3]: Order(x) + x**2
Out[3]: O(x)
In [4]: Order(x) + 28
Out[4]: 28 + O(x)Magma
LTaylor(L,s0,n) : LSer, FldComElt, RngIntElt -> FldComElt computes the first n + 1 terms of the Taylor expansion of the L-function about the point s=s0, where s0 is a complex number.
> E := EllipticCurve([0, 0, 1, -7, 6]); # define an elliptic curve E
> L := LSeries(E : Precision:=15);
> LTaylor(L, 1, 5 : ZeroBelow:=3);
1.73184990011930*$.1^3 - 3.20590558844390*$.1^4 + 2.80009237167013*$.1^5 + O($.1^9)SymPy
The integrals module in SymPy implements methods calculating definite and indefinite integrals of expressions. Principal method in this module is integrate():
- integrate(f, x) returns the indefinite integral
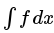
- integrate(f, (x, a, b)) returns the definite integral
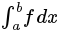
SymPy can integrate:
- polynomial functions:
In [6]: from sympy import *
In [7]: import sys
In [8]: from sympy import init_printing
In [9]: init_printing(use_unicode=False, wrap_line=False, no_global=True)
In [10]: x = Symbol('x')
In [11]: integrate(x**2 + 2*x + 4, x)
3
x 2
── + x + 4⋅x
3 - rational functions:
In [1]: integrate((x+1)/(x**2+4*x+4), x)
Out[1]:
1
log(x + 2) + ─────
x + 2- exponential-polynomial functions:
In [5]: integrate(5*x**2 * exp(x) * sin(x), x)
Out[5]:
2 x 2 x x x
5⋅x ⋅ℯ ⋅sin(x) 5⋅x ⋅ℯ ⋅cos(x) x 5⋅ℯ ⋅sin(x) 5⋅ℯ ⋅cos(x)
────────────── - ────────────── + 5⋅x⋅ℯ ⋅cos(x) - ─────────── - ──────────
2 2 2 2 - non-elementary integrals:
In [11]: integrate(exp(-x**2)*erf(x), x)
___ 2
╲╱ π ⋅erf (x)
─────────────
4 Here is an example of a definite integral (Calculate 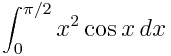 ):
):
In [1]: integrate(x**2 * cos(x), (x, 0, pi/2))
Out[1]:
2
π
-2 + ──
4Magma
Magma doesn't have support for integration.
SymPy
In [1]: from sympy import Symbol, exp, I
In [2]: x = Symbol("x")
In [3]: exp(I*2*x).expand()
Out[3]:
2⋅ⅈ⋅x
ℯ
In [4]: exp(I*2*x).expand(complex=True)
Out[4]:
-2⋅im(x) -2⋅im(x)
ⅈ⋅ℯ ⋅sin(2⋅re(x)) + ℯ ⋅cos(2⋅re(x))
In [5]: x = Symbol("x", real=True)
In [6]: exp(I*2*x).expand(complex=True)
Out[6]: ⅈ⋅sin(2⋅x) + cos(2⋅x)
In [7]: exp(-2 + 3*I*x).expand(complex=True)
Out[7]:
-2 -2
ⅈ⋅ℯ ⋅sin(3⋅x) + ℯ ⋅cos(3⋅x)Complex number division in iSymPy:
In [4]: from sympy import I
In [5]: ((2 + 3*I)/(3 + 7*I)).expand(complex=True)
Out[5]:
27 5⋅ⅈ
── - ───
58 58Magma
ComplexField(R) : FldRe -> FldCom returns the complex field which has real subfield R; in other words, the function returns the complex field with the same precision as the real field R.
> C<i> := ComplexField(10);
> Pi(C)+ 1/4*i;
> C<i> := ComplexField(10);
> (2 + 3*i)/(3 + 7*i);
0.4655172414 - 0.08620689655*iSymPy
trigonometric
In [1]: cos(x-y).expand(trig=True)
Out[1]: sin(x)⋅sin(y) + cos(x)⋅cos(y)
In [2]: cos(2*x).expand(trig=True)
Out[2]:
2
2⋅cos (x) - 1
In [3]: sinh(I*x**2)
Out[3]:
⎛ 2⎞
ⅈ⋅sin⎝x ⎠
In [11]: sinh(acosh(x))
Out[11]:
_______ _______
╲╱ x - 1 ⋅╲╱ x + 1 zeta function
In [4]: zeta(5, x**2)
Out[4]:
⎛ 2⎞
ζ⎝5, x ⎠
In [5]: zeta(5, 2)
Out[5]: ζ(5, 2)
In [6]: zeta(4, 1)
Out[6]:
4
π
──
90
In [5]: zeta(28).evalf()
Out[5]: 1.00000000372533factorials and gamma function
In [7]: a = Symbol('a')
In [8]: b = Symbol('b', integer=True)
In [9]: factorial(a)
Out[9]: a!
In[10]: factorial(10)
Out[10]: 3628800
In [11]: N(gamma(S(25)/10), 31)
Out[11]: 1.329340388179137020473625612506polynomials
In [14]: chebyshevt(8,x)
Out[14]:
8 6 4 2
128⋅x - 256⋅x + 160⋅x - 32⋅x + 1
In [15]: legendre(3, x)
Out[15]:
3
5⋅x 3⋅x
──── - ───
2 2
In [16]: hermite(3, x)
Out[16]:
3
8⋅x - 12⋅xMagma
trigonometric
Magma only has numerical values for the trigonometric functions.
> Sin(Sqrt(2)/2);
0.649636939080062444129478616044zeta function
RiemannZeta() : -> LSer returns the Riemann zeta function ζ(s). The number of digits of precision to which the values ζ(s) are to be computed may be specified using the Precision parameter. If it is omitted, the precision of the default real field will be used.
> L := RiemannZeta( : Precision:=40);
> Evaluate(L,2);
1.644934066848226436472415166646025189219
> Pi(RealField(40))^2/6;
1.644934066848226436472415166646025189219
> L := RiemannZeta( : Precision:=30);
> Evaluate(L,28);
1.00000000372533402478845705482factorials and gamma function
Factorial(n) : RngIntElt -> RngIntElt returns the factorial n! for positive small integer n.
> Factorial(10);
3628800Gamma(f) : RngSerElt -> RngSerElt returns the Gamma function Γ(f) of the series f. f must be defined over the free real or complex field, the valuation of f must be 0 and the constant term of f must be 1.
> Gamma(25/10);
1.32934038817913702047362561251polynomials
ChebyshevT(n) : RngIntElt -> RngUPolElt constructs the Chebyshev polynomial of the first kind Tn(x), where Tn(x) is defined by Tn(x) = cos n θwith x = cos θ.
> ChebyshevT(8);
128*$.1^8 - 256*$.1^6 + 160*$.1^4 - 32*$.1^2 + 1LegendrePolynomial(n) : RngIntElt -> RngUPolElt constructs the Legendre polynomial Pn(x) of degree n, where Pn(x) is defined by eqalign(P0(x) &= 1, P1(x) = x, cr Pn(x) &= (1 /(n)) ((2n - 1) x Pn - 1(x) - (n - 1) Pn - 2(x)).)
> LegendrePolynomial(3);
5/2*$.1^3 - 3/2*$.1HermitePolynomial(n) : RngIntElt -> RngUPolElt constructs the Hermite polynomial Hn(x) of degree n, where Hn(x) is defined by eqalign(H0(x) &= 1, H1(x) = 2x, cr Hn(x) &= 2x Hn - 1(x) - 2n Hn - 2(x).)
> HermitePolynomial(3);
8*$.1^3 - 12*$.1SymPy
In iSymPy:
In [10]: f(x).diff(x, x) + f(x)
Out[10]:
2
d
f(x) + ───(f(x))
2
dx
In [11]: dsolve(f(x).diff(x, x) + f(x), f(x))
Out[11]: f(x) = C₁⋅sin(x) + C₂⋅cos(x)Magma
Differential(s) : RngDiffElt -> RngDiffElt returns the differential of s in the algebraic differential field F, as a differential in the differential space of the underlying ring of F.
> F<z> := RationalDifferentialField(Rationals());
> Differential(z);
(1) d(z)
> Differential(1/z+6+5*z);
((5*z^2 - 1)/z^2) d(z)SymPy
In iSymPy:
In [3]: solve(x**3 + 2*x**2 - 1, x)
Out[3]:
⎡ ___ ___ ⎤
⎢ 1 ╲╱ 5 ╲╱ 5 1⎥
⎢-1, - ─ + ─────, - ───── - ─⎥
⎣ 2 2 2 2⎦
In [5]: solve( [x**2 + 4*y**2 -2, -10*x + 2*y -15], [x, y])
Out[5]:
⎡⎛ ____ ____ ⎞ ⎛ ____ ____ ⎞⎤
⎢⎜ 150 ╲╱ 23 ⋅ⅈ 15 5⋅╲╱ 23 ⋅ⅈ ⎟ ⎜ 150 ╲╱ 23 ⋅ⅈ 15 5⋅╲╱ 23 ⋅ ⎟⎥
⎢⎜- ─── - ────────, ─── - ──────────⎟, ⎜- ─── + ────────, ─── + ────────── ⎟⎥
⎣⎝ 101 101 202 101 ⎠ ⎝ 101 101 202 101 ⎠⎦ Magma
Magma doesn't have support for algebraic equations.
SymPy
In SymPy, matrices are created as instances from the Matrix class:
In [1]: from sympy import Matrix
In [2]: Matrix([ [1, 0 , 0], [0, 1, 0], [0, 0, 1] ])
Out[2]:
⎡1 0 0⎤
⎢ ⎥
⎢0 1 0⎥
⎢ ⎥
⎣0 0 1⎦It is possible to slice submatrices, since this is Python:
In [4]: M = Matrix(2, 3, [1, 2, 3, 4, 5, 6])
In [5]: M[0:2,0:2]
Out[5]:
⎡1 2⎤
⎢ ⎥
⎣4 5⎦
In [6]: M[1:2,2]
Out[6]: [6]
In [7]: M[:,2]
Out[7]:
⎡3⎤
⎢ ⎥
⎣6⎦One basic operation involving matrices is the determinant:
In [8]: M = Matrix(( [2, 5, 6], [4, 7, 10], [1, 0, 3] ))
In [9]: M.det()
Out[9]: -10print_nonzero(symb='x') shows location of non-zero entries for fast shape lookup.
In [10]: M = Matrix(( [2, 0, 0, 1, 0], [3, 5, 0, 1, 0], [10, 4, 0, 1, 2], [1, 6, 0, 0, 0], [0, 4, 0, 2, 2] ))
In [12]: M
Out[12]:
⎡2 0 0 1 0⎤
⎢ ⎥
⎢3 5 0 1 0⎥
⎢ ⎥
⎢10 4 0 1 2⎥
⎢ ⎥
⎢1 6 0 0 0⎥
⎢ ⎥
⎣0 4 0 2 2⎦
In [13]: M.print_nonzero()
[X X ]
[XX X ]
[XX XX]
[XX ]
[ X XX]Matrix transposition with transpose():
In [14]: from sympy import Matrix, I
In [15]: m = Matrix(( (1,2+I), (3,4) ))
In [16]: m
Out[16]:
⎡1 2 + ⅈ⎤
⎢ ⎥
⎣3 4 ⎦
In [17]: m.transpose()
Out[17]:
⎡ 1 3⎤
⎢ ⎥
⎣2 + ⅈ 4⎦
In [19]: m.T == m.transpose()
Out[19]: TrueThe multiply_elementwise(b) method returns the Hadamard product (elementwise product) of A and B:
In [14]: import sympy
In [15]: A = sympy.Matrix([ [1, 3, 20], [1, 18, 3] ])
In [17]: B = sympy.Matrix([ [0, 5, 10], [4, 20, 6] ])
In [18]: print A.multiply_elementwise(B)
[0, 15, 200]
[4, 360, 18]Magma
Matrix(R, m, n, Q) : Rng, RngIntElt, RngIntElt, [ RngElt ] -> Mtrx is used in Magma to construct matrices.
> X := Matrix(IntegerRing(), 3, 3, [1, 0, 0, 0, 1, 0, 0, 0, 1]); # create the identity matrix of degree 3
> X;
[1 0 0]
[0 1 0]
[0 0 1]
> Parent(X);
Full Matrix Algebra of degree 3 over Integer RingMagma can also create special matrices:
> D := DiagonalMatrix(GF(23), [2, 4, 6]); # define a 3 x 3 diagonal matrix over GF(23)
> D;
[ 2 0 0]
[ 0 4 0]
[ 0 0 6]
> Parent(D);
Full Matrix Algebra of degree 3 over GF(23)
> S := SymmetricMatrix([1, 1/2, 3, 1, 3, 4]);
> S;
[ 1 1/2 1]
[1/2 3 3]
[ 1 3 4]
> Parent(S);
Full Matrix Algebra of degree 3 over Rational FieldMagma can construct random matrices with the help of several commands such as: RandomMatrix(R, m, n) : Rng, RngIntElt, RngIntElt -> Mtrx. Given a finite ring R and positive integers m and n, construct a random m x n matrix over R.
> R := RandomMatrix(GF(23), 3, 4);
> R;
[13 1 3 2]
[ 2 0 4 10]
[16 5 19 21]
> Parent(R);
Full KMatrixSpace of 3 by 4 matrices over GF(23)Transpose(A) : Mtrx -> Mtrx calculates the transpose of matrix A. Given an m x n matrix A over a ring R, return the transpose of A, which is simply the n x m matrix over R whose (i, j)-th entry is the (j, i)-th entry of A.
> A := Matrix(IntegerRing(), 4, 3, [6, 5, 4, 9, 8, 7, 1, 2, 3, 8, 7, 6]);
> A;
[6 5 4]
[9 8 7]
[1 2 3]
[8 7 6]
> Parent(A);
Full RMatrixSpace of 4 by 3 matrices over Integer Ring
> Transpose(A);
[6 9 1 8]
[5 8 2 7]
[4 7 3 6]The IsZero(A) : Mtrx -> BoolElt command returns true f A is the m x n zero matrix.
> A := Matrix(IntegerRing(), 2, 3, [ 0, 0, 0, 0, 0, 0 ]);
> A;
[0 0 0]
[0 0 0]
> Parent(A);
Full RMatrixSpace of 2 by 3 matrices over Integer Ring
> IsZero(A);
trueDeterminant(A: parameters) : Mtrx -> RngElt -> Given a square matrix A over the ring R, return the determinant of A as an element of R. R may be any commutative ring. The determinant of the 0 x 0 matrix over R is defined to be R! 1.
> A := Matrix(IntegerRing(), 3, 3, [2, 5, 6, 4, 7, 10, 1, 0, 3]);
> A;
[ 2 5 6]
[ 4 7 10]
[ 1 0 3]
> Determinant(A);
-10SymPy
The geometry module can be used to create two-dimensional geometrical entities and query information about them. These entities are available:
- Point
- Line, Ray, Segment
- Ellipse, Circle
- Polygon, RegularPolygon, Triangle
Check if points are collinear:
In [37]: from sympy import *
In [38]: from sympy.geometry import *
In [39]: x = Point(0, 0)
In [40]: y = Point(3, 1)
In [41]: z = Point(5, 5)
In [42]: Point.is_collinear(x, y, z)
Out[42]: False
In [43]: Point.is_collinear(x, z)
Out[43]: TrueSegment declaration, slope, length, midpoint:
In [1]: import sympy
In [2]: from sympy import Point
In [3]: from sympy.abc import s
In [4]: from sympy.geometry import Segment
In [5]: Segment( (1, 2), (2, -3))
Out[5]: ((1,), (2,))
In [6]: s = Segment(Point(4, 3), Point(1, 1))
In [7]: s
Out[7]: ((1,), (4,))
In [8]: s.points
Out[8]: ((1,), (4,))
In [9]: s.slope
Out[9]: 2/3
In [10]: s.length
Out[10]:
____
╲╱ 13
In [11]: s.midpoint
Out[11]: (5/2,)Magma
The following example shows how points and lines of a plane can be created.
> P, V, L := FiniteProjectivePlane(5);
> V;
Point-set of Projective Plane PG(2, 5)
> L;
Line-set of Projective Plane PG(2, 5)
> V.3; #create the third point of P
( 0 : 0 : 1 )
> V![1, 4, 3]
( 1 : 4 : 3 )
> L.6; # create the sixth line of P
< 1 : 1 : 3 >
> L![4, 3, 2];
< 1 : 2 : 3 >
> K<w> := GF(4);
> P, V, L := FiniteProjectivePlane(K);
> l := L![1, 0, 1]; # create the line x + z = 0
> l;
< 1 : 0 : 1 >
> Coordinates(P, l); # get the coordinates of the line l
[ 1, 0, 1 ]
> V![1, 0, 1] in l; # test if a point is on the line l
true SymPy
Using the .match method and the Wild class you can perform pattern matching on expressions. The method returns a dictionary with the needed substitutions. Here is an example:
In [11]: from sympy import *
In [12]: x = Symbol('x')
In [13]: y = Wild('y')
In [14]: (10*x**3).match(y*x**3)
Out[14]: {y: 10}
In [15]: s = Wild('s')
In [16]: (x**4).match(y*x**s)
Out[16]: {s: 4, y: 1}SymPy returns None if the match is unsuccessful:
In [19]: print (x+1).match(y**x)
NoneMagma
Match(u, v, f) : GrpFPElt, GrpFPElt, RngIntElt -> BoolElt, RngIntElt returns the value true if it has found an integer. If Match hasn't found the integer, it returns the value false.
> b, p := Match(w, u, 1);
> b, p;
true 4SymPy
There are many ways of printing mathematical expressions. Three of the most common methods are:
- Standard printing
- Pretty printing using the pprint() function
- Pretty printing using the init_printing() method
Standard printing is the return value of str(expression):
>>> from sympy import Integral # Python session
>>> from sympy.abc import c
>>> print c**3
c**3
>>> print 2/c
2/c
>>> print Integral(c**2+2*c, c)
Integral(c**2 + 2*c, c)Pretty printing is a nice ascii-art printing with the help of a pprint function.
In [1]: from sympy import Integral, pprint # IPython session (pprint enabled by default)
In [2]: from sympy.abc import c
In [3]: pprint(c**3)
3
c
In [4]: pprint(2/c)
2
─
c
In [5]: pprint(Integral(c**2+2*c, c))
⌠
⎮ ⎛ 2 ⎞
⎮ ⎝c + 2⋅c⎠ dc
⌡ However, the proper way to set up pretty printing in SymPy is to use init_printing(pretty_print=True, order=None, use_unicode=None, wrap_line=None, num_columns=None, no_global=False, ip=None):
>>> from sympy import init_printing
>>> init_printing(use_unicode=False, wrap_line=False, no_global=True)
>>> from sympy import Integral, Symbol
>>> x = Symbol('x')
>>> Integral(x**3+2*x+1, x)
/
|
| / 3 \
| \x + 2*x + 1/ dx
|
/
>>> init_printing(pretty_print=True)
>>> Integral(x**3+2*x+1, x)
⌠
⎮ ⎛ 3 ⎞
⎮ ⎝x + 2⋅x + 1⎠ dx
⌡Magma
You can print expressions in Magma in more ways:
A ` PrintStyle : AlgSym -> MonStgElt helps you to retrieve or set the style in which elements of the algebra A will print. The default is the leicographical ordering, "Lex". Other options are "Length" and "MaximalPart".
> M := SFAMonomial(Rationals());
> M`PrintStyle;
Lex
> P := Partitions(3);
> P;
[
[ 3 ],
[ 2, 1 ],
[ 1, 1, 1 ]
]
> f := &+[M.p : p in P];
> f;
M.[1,1,1] + M.[2,1] + M.[3]
> M`PrintStyle := "Length";
> f;
M.[3] + M.[2,1] + M.[1,1,1]
> M`PrintStyle := "MaximalPart";
> f;
M.[1,1,1] + M.[2,1] + M.[3]print expression : parameters; prints the value of the expression. There are four levels of printing that may be indicated after the colon: Default, Minimal, Maximal and Magma.
> F<t> := FunctionField(RationalField());
> f := (1/((t^2+2*t+1)*(t^2-1)));
> print f : Magma;
1/(t^4 + 2*t^3 - 2*t - 1)printf format, expression, ..., expression; prints values of the expressions under control of format.
> for i := 1 to 150 by 33 do printf "[%3o]\n", i; end for;
[ 1]
[ 34]
[ 67]
[100]
[133]
> for i := 1 to 150 by 33 do printf "[%-3o]\n", i; end for;
[1 ]
[34 ]
[67 ]
[100]
[133]
> for w := 1 to 5 do printf "[%*o]", w, 1; end for;
[1][ 1][ 1][ 1][ 1]SymPy
Pyglet is required to use the plotting function of SymPy in 2d and 3d. Here is an example:
>>> from sympy import symbols, Plot, cos, sin
>>> x, y = symbols('x y')
>>> Plot(sin(x*10)*cos(y*5) - x*y)
[0]: -x*y + sin(10*x)*cos(5*y), 'mode=cartesian'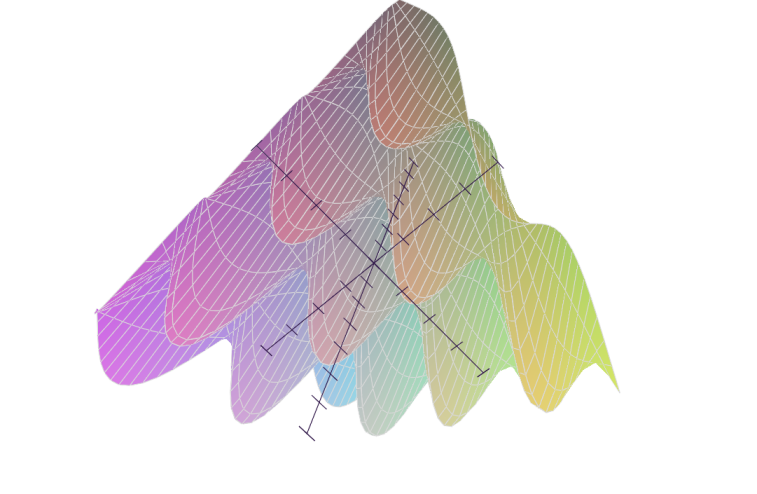
In[1]: Plot(cos(x*y*10))
Out[1]: [0]: cos(10*x*y), 'mode=cartesian'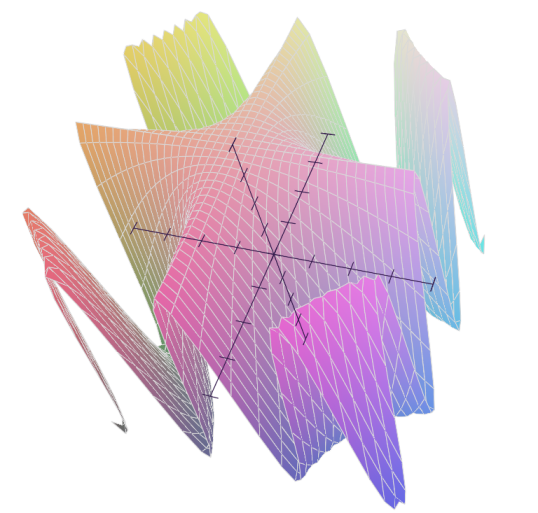
In [22]: Plot(1*x**2, [], [x], 'mode=cylindrical') # [unbound_theta,0,2*Pi,40], [x,-1,1,20]
Out[22]: [0]: x**2, 'mode=cylindrical'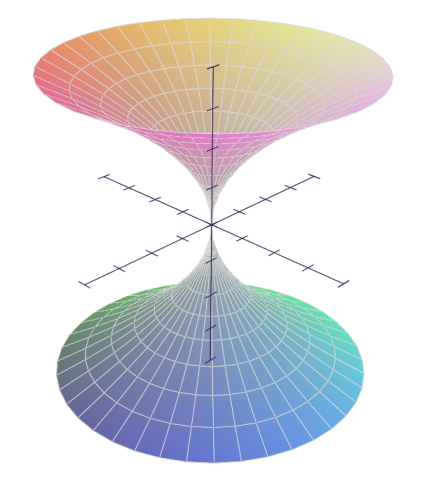
Magma
Magma doesn't have support for plotting.
SymPy aims to be a lightweight normal Python module so as to become a nice open source alternative to Maple/Mathematica. Its goal is to be reasonably fast, easily extended with your own ideas, be callable from Python and could be used in real world problems. SymPy is perfectly multiplatform, it's small and easy to install and use, since it is written in pure Python (and doesn't need anything else).
You can choose to use either SymPy or Magma, depending on what your needs are. SymPy is used for general-purpose computing, while Magma is for research with the use of advanced algebra. For more information you can go to the official sites of SymPy and Magma.